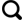童庆禧,张兵,郑兰芬
1
2006
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Hyperspectral Unmixing Overview: Geometrical,Statistical,and Sparse Regression-based Approaches
5
2012
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
... [2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
... [2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
... 对于以图像中纯像元是否存在来划分的这两大类光谱解混方法,从计算量和算法意义的角度来看,满足纯像元存在假设类方法只需进行单形体体积计算和比较,其物理意义明确,因此相较后者具有计算量小、算法优化设计多等优点[2],但是在实际应用中,多数场景纯像元假设条件难以满足,会影响端元提取的精度;而后者则从图像中估计端元矩阵,适用于更多的场景,但需要采用优化方法对目标函数进行迭代求解,导致这类算法计算量偏大.同时,无论是端元提取还是端元生成方法,均容易受到图像噪声、异常点的影响,所幸已有方法[87,90]针对这类问题进行了探索,但由于噪声在真实数据中的广泛存在,这类克服噪声等干扰信息的方法还需进一步深入研究. ...
Linear Mixing and The Estimation of Ground Cover Proportions
1
1993
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Sparse Unmixing of Hyperspectral Data Using Spectral a Priori Information
1
2015
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Sub-pixel Mineral Mapping of a Porphyry Copper Belt Using EO-1 Hyperion Data
1
2014
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Multiscale Quantification of Urban Composition from EO-1/Hyperion Data Using Object-based Spectral Unmixing
1
2016
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Applying Linear Spectral Unmixing to Airborne Hyperspectral Imagery for Mapping Yield Variability in Grain Sorghum and Cotton Fields
1
2010
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
Spectral Unmixing
2
2002
... 高/多光谱图像中混合像元的存在,使得传统的像素级遥感图像分类方法受到局限,限制了高光谱遥感图像的精细化、定量化处理和应用[1-2].光谱解混技术正是针对高/多光谱遥感图像中大量存在的混合像元而提出的一种信号分离技术[3].由于光谱解混可得到单个像元内更量化、更精细的地物信息,也有学者称其为亚像元分类技术[4].目前,光谱解混技术已经在地质勘探[5]、城市调查[6]以及农作物监测[7]等遥感应用领域发挥了重要作用.光谱解混技术根据处理链路包括数据降维、端元获取和丰度估计等处理步骤[2,8],其中端元获取和丰度估计是光谱解混的重要环节.相较传统的光学全色图像,高光谱图像光谱解混技术可获取图像中的亚像元地物信息,其深入研究可进一步提升的高光谱图像精细化、定量化应用水平,对促进高光谱遥感数据在国民生产、军事侦察领域的推广应用具有重要的作用. ...
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
基于光谱和空间信息的高光谱图像解混方法研究
1
2016
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
基于光谱和空间信息的高光谱图像解混方法研究
1
2016
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
高光谱遥感影像端元提取算法研究进展及分类
1
2015
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
高光谱遥感影像端元提取算法研究进展及分类
1
2015
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
基于离散粒子群算法的凸多模态高光谱图像端元提取研究
1
2018
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
基于离散粒子群算法的凸多模态高光谱图像端元提取研究
1
2018
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
Comparative Study and Analysis among ATGP, VCA, and SGA for Finding Endmembers in Hyperspectral Imagery
3
2016
... 一直以来,光谱解混技术是国内外高光谱遥感领域的研究热点[2,8],已报道方法根据建模差异可分为线性和非线性光谱解混两大类.前者研究众多,形成了主流的基于统计、稀疏回归以及凸体几何的处理方法[2],其中凸体几何类方法由于直观性强、易理解、计算量小受到了广泛关注[9],涌现出许多研究成果.本文结合国内学者的一些研究报道[10-12],着重从凸体建模求解方法(投影、凸锥以及单形体体积[13])和纯像元存在假设两个角度对国内外凸体几何高光谱图像光谱解混方法进行回顾,并对该类方法中的几个关键问题进行初步分析,以期为光谱解混方法的研究、学习和应用提供参考. ...
... 基于正交投影、凸锥以及单形体体积来划分的光谱解混方法在丰度非负(Abundance Nonnegativity Constraint, ANC)和丰度和为一(Abundance Sum-to-one Constraint, ASC)两个物理约束方面存在差异.Chang等[13]指出,正交投影方法为无约束方法,凸锥类方法则考虑非负约束,而单形体体积类方法则考虑了ANC和ASC两个约束,并证明了投影类ATGP方法与体积类SGA方法存在等价关系.这三类方法在三维空间中的几何描述如图1所示,投影类方法在图像的特征空间寻找某个向量V,将像元向量对其投影求解极值作为端元;凸锥方法认为在正象限,非负像元光谱向量构建了O-ABC非封闭凸锥,试图寻找凸锥的OA、OB、OC边界向量作为端元;单形体体积则通过像元向量在子空间中张成的单形体的体积来获取端元,图(1)中最大体积方法求解A、B、C以及pi像元中由3个像元构建的最大三角形面积,由于三角形ABC面积最大,OA、OB、OC为最终获得的端元向量. ...
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Simple Models for Complex Natural Surfaces: A Strategy for The Hyperspectral Era of Remote Sensing
1
1989
... 基于Adams高光谱图像线性混合模型[14]与凸集在数学表达上的等价性,以及Craig最小单形体[15]思想,Boardman最早将凸体几何理论[16]引入到高光谱图像光谱解混研究,该理论是凸体几何光谱解混研究的重要里程碑.总的来看,凸体几何光谱解混方法的发展脉络可按不同的研究角度来梳理,一种按正交投影、凸锥以及单形体体积等凸体建模求解方法进行划分,另一种则以图像中是否存在纯像元为条件来划分. ...
Unsupervised Unmixing of Remotely Sensed Images
1
1990
... 基于Adams高光谱图像线性混合模型[14]与凸集在数学表达上的等价性,以及Craig最小单形体[15]思想,Boardman最早将凸体几何理论[16]引入到高光谱图像光谱解混研究,该理论是凸体几何光谱解混研究的重要里程碑.总的来看,凸体几何光谱解混方法的发展脉络可按不同的研究角度来梳理,一种按正交投影、凸锥以及单形体体积等凸体建模求解方法进行划分,另一种则以图像中是否存在纯像元为条件来划分. ...
Automating Spectral Unmixing of AVIRIS Data Using Convex Geometry Concepts
1
1993
... 基于Adams高光谱图像线性混合模型[14]与凸集在数学表达上的等价性,以及Craig最小单形体[15]思想,Boardman最早将凸体几何理论[16]引入到高光谱图像光谱解混研究,该理论是凸体几何光谱解混研究的重要里程碑.总的来看,凸体几何光谱解混方法的发展脉络可按不同的研究角度来梳理,一种按正交投影、凸锥以及单形体体积等凸体建模求解方法进行划分,另一种则以图像中是否存在纯像元为条件来划分. ...
Mapping Target Signatures via Partial Unmixing of AVIRIS Data
1
1995
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
A Fast Iterative Algorithm for Implementation of Pixel Purity Index
1
2006
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Random Pixel Purity Index Algorithm
1
2010
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Design and Development of Iterative Pixel Purity Index
1
2015
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
基于空间像素纯度指数的端元提取算法
1
2013
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
基于空间像素纯度指数的端元提取算法
1
2013
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Vertex Component Analysis: A Fast Algorithm to Unmix Hyperspectral Data
1
2005
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Automatic Spectral Target Recognition in Hyperspectral Imagery
1
2003
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Recursive Orthogonal Projection-based Simplex Growing Algorithm
1
2016
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Hyperspectral Image Classification and Dimensionality Reduction: An Orthogonal Subspace Projection Approach
1
1994
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Endmember Extraction for Hyperspectral Image Analysis
3
2008
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
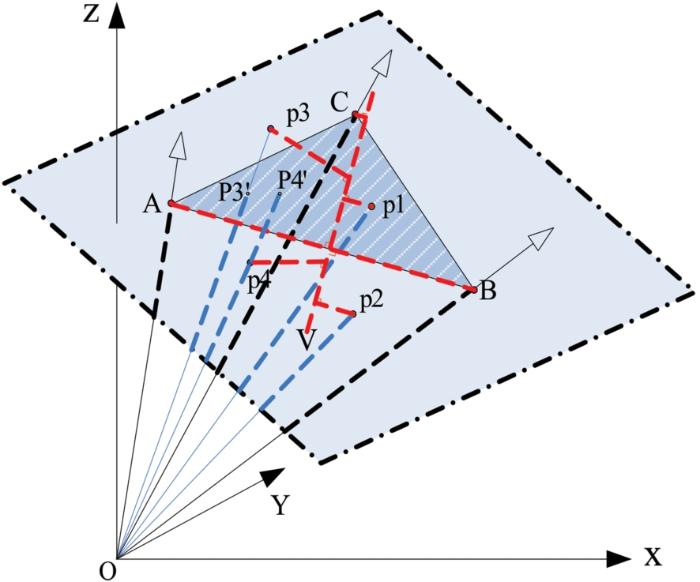
... 数据降维处理在高光谱图像处理过程中可降低计算开销,同时也可满足N-FINDR、SGA等经典算法利用行列式进行单形体体积计算时的方阵所需,是一种经常被采用的高光谱图像处理方法.典型的数据降维方法主要有主成分分析(PCA)[91]、最大噪声分离(MNF)[92]等.通常情况下,数据降维处理会造成一些小目标信息的损失[93],但是,也有学者认为数据降维可提升端元提取算法的性能[26].针对不同噪声条件下数据降维对凸体几何类端元提取方法的影响,本文采用模拟数据对3种比较典型的端元提取方法ATGP(投影)、N-FINDR(体积)以及CCVA(凸锥)进行验证.模拟数据采用公式(1)生成: ...
非监督正交子空间投影的高光谱混合像元自动分解
1
2004
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
非监督正交子空间投影的高光谱混合像元自动分解
1
2004
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
一种正交子空间投影高光谱图像端元提取算法
1
2016
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
一种正交子空间投影高光谱图像端元提取算法
1
2016
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
一种基于端元投影向量的高光谱图像地物提取算法
1
2005
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
一种基于端元投影向量的高光谱图像地物提取算法
1
2005
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
高光谱遥感图像端元提取的零空间光谱投影算法
1
2010
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
高光谱遥感图像端元提取的零空间光谱投影算法
1
2010
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Orthogonal bases Approach for The Decomposition of Mixed Pixels in Hyperspectral Imagery
1
2009
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
基于数据空间正交基的遥感图像混合像元分解新方法
1
2009
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
基于数据空间正交基的遥感图像混合像元分解新方法
1
2009
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
用于光谱解混的正交向量投影算法
1
2015
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
用于光谱解混的正交向量投影算法
1
2015
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Fully Constrained Least Squares Spectral Unmixing by Simplex Projection
2
2011
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
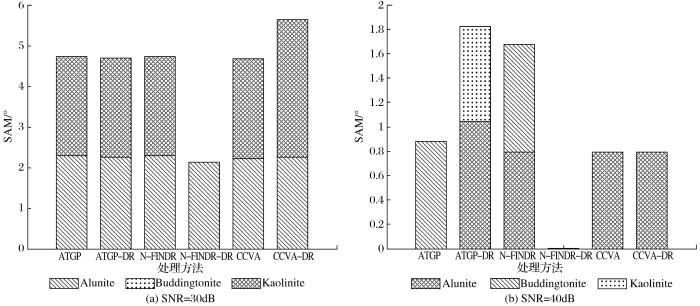
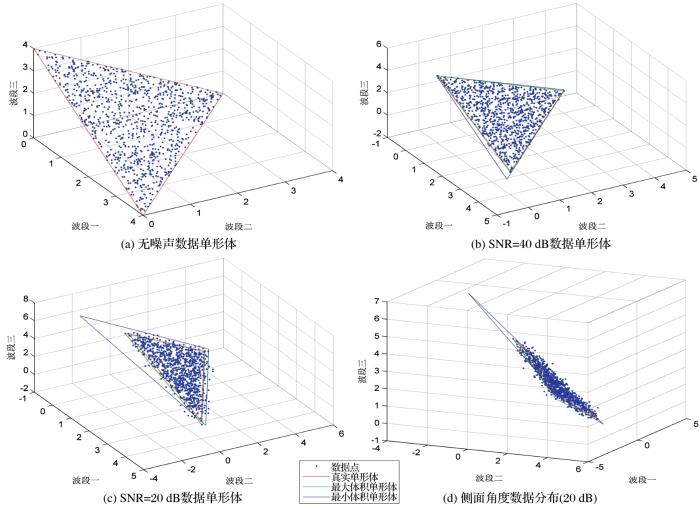
... 在单形体体积类光谱解混方法中,最大体积和最小体积包裹为两类经典方法,也是凸体体积类光谱解混方法的两个体积标准.最大体积以端元存在假设为前提,通过计算所有像元张成单形体的最大体积来得到指定个数的端元;而最小体积包裹标准则无需纯像元假设,通过计算包裹所有像元的向量作为虚拟端元.容易理解,在无噪声的理想状态下,最大体积和最小体积标准可获得一致结果.实验采用的无噪声模拟数据如图3(a)所示,在加入不同量级噪声(信噪比SNR=20 dB、40 dB)的情况下,采用两类体积标准得到结果如图3(b)和(c)所示,可看出,在噪声存在情况下,部分数据点外溢到真实单形体之外,从而导致计算得到的最大体积和最小体积包裹均与真实单形体有所差异.从实验结果来看,最小体积包裹标准获得的单形体均偏大;而最大体积标准获得的单形体在SNR为40dB时与真实单形体差异不大,但在SNR为20dB的时体积也明显偏大.另外,由于模拟数据生成时采用的丰度系数满足狄利克雷分布,因此在无噪声条件下,图3(a)中的数据在同一平面上,而加入噪声后,模拟数据不再满足ASC和ANC,SNR为20 dB模拟数据的某视角可看出其数据点不在一个平面内(图3(d)),因此,当采用凸体几何类方法进行丰度系数求解时,需要对这类单形体之外的数据点(外点)进行重点考虑,例如SPU[34]采用迭代投影来实现这些外点向单形体面的投影,再对投影后的数据点进行丰度估计. ...
A New Fast Algorithm for Linearly Unmixing Hyperspectral Images
1
2015
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Recursive Geometric Simplex Growing Analysis for Finding Endmembers in Hyperspectral Imagery
1
2017
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
Geometric N-Finder Algorithm for Finding Endmembers in Hyperspectral Imagery
1
2017
... 正交投影(Orthogonal Projection, OP)将像元向量向某个指定向量或子空间进行投影,通过判断投影值大小来实现光谱解混(如图1所示).像元纯净指数[17](Pixel Purity Index, PPI)将像元向量投影到随机单位向量并记录极值来获取端元,后续出现了快速迭代FIPPI[18]、随机RPPI[19]、优化迭代PPI(IPPI)[20]以及空间邻域SPPI[21]等多种优化算法;VCA(Vertex Component Analysis)[22]和ATGP(Automatic Target Generation Process)[23]将图像像元向已知端元张成的正交子空间进行投影,求取最大投影值像元作为新的端元,但二者在正交处理等方面存在差异[13];OP-SGA(OP-Simplex Growth Algorithm)[24]端元提取算法将SGA的单形体体积计算简化为像元向量与已知端元基向量的OP计算;SPA(Successive Projection Algorithm)则结合了OP与像元光谱的空间邻域特性.施密特正交化(Gram-Schmidt Orthogonalization,GSO)用于向量组的正交化变换,与正交子空间投影(Orthogonal Subspace Projection, OSP)[25]存在等价关系[26],因此本文将OSP、GSO类方法也归入到正交投影一类.在OSP、GSO的光谱解混应用方面,国内有学者提出了非监督正交子空间投影光谱解混方法(UOSP)[27]、最小光谱信息墒OSP[28]以及采用GSO获取端元投影向量[29]的方法,而零空间投影算法[30]是一种与OSP算子相似的端元提取方法.其后,国内学者又提出了采用正交基分析[31-32](Orthogonal Bases Approach, OBA)、GSO向量投影的丰度估计[33]方法.在国外,Heylen等[34]提出的单形体投影(SPU)全约束丰度估计方法可提升端元提取和丰度估计的效率.在OBA基础上,FUN[35](Fast UNmixing)方法采用改进GSO方法来进行高光谱图像的端元提取和丰度估计.近期出现的几何-SGA(Geometric-SGA)方法则从简化体积计算等角度,采用GSO对SGA算法进行优化[36].近期,GSO被用于代替传统N-FINDR算法的降维处理和体积计算,从而优化计算效率[37]. ...
N-FINDR: An Algorithm for Fast Autonomous Spectral Endmember Determination in Hyperspectral Data
1
1999
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A New Growing Method for Simplex-based Endmember Extraction Algorithm
1
2006
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A Novel Geometry-based Feature-selection Technique for Hyperspectral Imagery
1
2007
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Sequential N-FINDR algorithm
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Using a New Search Strategy to Improve the Performance of N-FINDR Algorithm for End-Member Determination
1
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Fast Algorithms to Implement N-FINDR for Hyperspectral Endmember Extraction
2
2011
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
... [43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Random N-Finder (N-FINDR) Endmember Extraction Algorithms for Hyperspectral Imagery
1
2011
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Reducing the Complexity of the N-FINDR Algorithm for Hyperspectral Image Analysis
1
2013
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Modified N-FINDR Endmember Extraction Algorithm for Remote Sensing Imagery
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于代数余子式的N-FINDR快速端元提取算法
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于代数余子式的N-FINDR快速端元提取算法
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种改进的快速N-FINDR端元提取算法
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种改进的快速N-FINDR端元提取算法
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A Quantitative and Comparative Analysis of Different Implementations of N-FINDR: A Fast Endmember Extraction Algorithm
1
2009
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种改进的N-FINDR高光谱端元提取算法
1
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种改进的N-FINDR高光谱端元提取算法
1
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Real-Time Simplex Growing Algorithms for Hyperspectral Endmember Extraction
1
2010
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于Cayley-Menger行列式的高光谱遥感图像端元提取方法
2
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
... 在已知单形体各棱边边长的情况下,可采用Cayley-Menger行列式来计算单形体体积,该公式也被用于高光谱图像端元提取[52],由于矩阵元素采用n个端元光谱向量间的相互距离,因此必然为方阵(公式(4)),无需对高光谱图像进行降维处理. ...
基于Cayley-Menger行列式的高光谱遥感图像端元提取方法
2
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
... 在已知单形体各棱边边长的情况下,可采用Cayley-Menger行列式来计算单形体体积,该公式也被用于高光谱图像端元提取[52],由于矩阵元素采用n个端元光谱向量间的相互距离,因此必然为方阵(公式(4)),无需对高光谱图像进行降维处理. ...
Triangular Factorization based Simplex Algorithms for Hyperspectral Unmixing
1
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Progressive Band Processing of Simplex Growing Algorithm for Finding Endmembers in Hyperspectral Imagery
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A Fast Endmember Extraction Algorithm based on Gram Determinant
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
快速实现基于单形体体积生长的端元提取算法
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
快速实现基于单形体体积生长的端元提取算法
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
从端元选择到光谱解混的距离测算方法
1
2010
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
从端元选择到光谱解混的距离测算方法
1
2010
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Kernel Simplex Growing Algorithm for Hyperspectral Endmember Extraction
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于零空间最大距离的高光谱图像端元提取算法
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于零空间最大距离的高光谱图像端元提取算法
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Minimum-volume Transforms for Remotely Sensed Data
1
1994
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Endmember Extraction from Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization
1
2007
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A Convex Analysis-based Minimum-Volume Enclosing Simplex Algorithm for Hyperspectral Unmixing
1
2009
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Minimum Volume Simplex Analysis: A Fast Algorithm to Unmix Hyperspectral Data
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Minimum Volume Simplex Analysis: A Fast Algorithm for Linear Hyperspectral Unmixing
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Chance-Constrained Robust Minimum-Volume Enclosing Simplex Algorithm for Hyperspectral Unmixing
1
2011
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A New Minimum-Volume Enclosing Algorithm for Endmember Identification and Abundance Estimation in Hyperspectral Data
1
2012
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A Fast Hyperplane-based Minimum-Volume Enclosing Simplex Algorithm for Blind Hyperspectral Unmixing
1
2016
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Robust Minimum Volume Simplex Analysis for Hyperspectral Unmixing
1
2017
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种自适应鲁棒最小体积高光谱解混算法
1
2017
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种自适应鲁棒最小体积高光谱解混算法
1
2017
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种利用单形体体积自动提取高光谱图像端元的算法
1
2006
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种利用单形体体积自动提取高光谱图像端元的算法
1
2006
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种基于高维空间凸面单形体体积的高光谱图像解混算法
1
2004
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
一种基于高维空间凸面单形体体积的高光谱图像解混算法
1
2004
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Geometric Unmixing of Large Hyperspectral Images: A Barycentric Coordinate Approach
1
2012
... 从另一个角度—图像中纯像元存在假设,也可对凸体几何类端元获取方法进行划分,后续的丰度估计可采用最小二乘法[88]或凸体几何关系来求解[72].满足纯像元存在假设类方法以图像中至少存在一个纯像元为前提,通过高光谱图像的凸体几何结构特征分析,从图像中获取存在的纯像元,因此这类方法被称为端元提取,典型的方法有PPI、N-FINDR、SGA、CCVA及其优化方法等;而无需纯像元假设的算法适用于更多的场景,其通过建立凸体结构目标函数优化模型并求解来获取虚拟端元[89],这些端元是对图像中纯像元的估计,因此这类方法常被称为端元生成方法,典型的方法有MVES、MVSA等. ...
Subspace-Projection-based Geometric Unmixing for Material Quantification in Hyperspectral Imagery
1
2014
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于子空间距离的高光谱图像光谱解混算法
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
基于子空间距离的高光谱图像光谱解混算法
1
2008
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
A New Endmember Generation Algorithm based on a Geometric Optimization Model for Hyperspectral Images
1
2013
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Optimizing the Endmembers Using Volume Invariant Constrained Model
1
2015
... 单形体体积(Simplex Volume,SV)类方法根据纯像元存在假设条件可分为最大体积和最小体积包裹标准两类.最大体积类光谱解混方法通过单形体体积膨胀,获取最大单形体顶点作为端元,经典方法有N-FINDR[38]、SGA[39]方法.N-FINDR同步求解端元矩阵行列式的最大值来获取端元,而SGA是逐个求解端元的N-FINDR优化版本[26].以N-FINDR为引子,出现了以距离测度替换体积计算[40]、SeQuential N-FINDR(SQ N-FINDR)[41]、改进搜索策略的N-FINDR[42]、SuCcessive N-FINDR(SC N-FINDR)[43]、Iterative N-FINDR(IN-FINDR)[43]、Random N-FINDR[44]、矩阵分解LDU-N-FINDR[45]、丰度估计MN-FINDR[46]、代数余子式N-FINDR[47]、DN-FINDR[48]等效率优化方法,以及更换初始化条件[49]、引入支持向量机[50]等来提升N-FINDR精度的方法.以SGA为基础,出现了Real-Time SGA(RT SGA)[51]、辅助高Cayley-Menger行列式[52]、矩阵三角分解[53]、逐波段处理SGA(PBP-SGA)[54]、快速Gram行列式(FGDA)[55]、快速SGA[56]等提升计算速度,以及支持向量机SGA[57]、核SGA(Kernel New SGA,KNSGA)[58]等提升解混精度的方法.零空间最大距离端元提取方法[59]与最大体积方法原理相似,将体积简化为距离计算来提升效率.最小体积包裹类方法则求解包裹高光谱图像像元的最小单形体顶点作为虚拟端元,其以最小体积变换(Minimum Volume Transform, MVT)[60]为基础,后续出现了最小体积约束非负矩阵分解(MVC-NMF)[61]、最小体积包裹单形体(MVES)[62]、最小体积单形体分析(MVSA)[63-64]、Chance约束MVES[65]、MINVEST[66]、超平面MVES[67]、鲁棒MVES(RMVES)[68]、鲁棒最小体积解混(RMVHU)[69]等方法.另外,从单形体体积计算的角度,新的体积计算公式可消除降维对数据的影响[70],体积比/质心坐标[71-73]以及子空间距离[74]可以从凸体几何角度获取高光谱图像丰度系数,几何优化模型(GOM)[75]利用体积比的ASC约束进行端元估计,体积不变约束几何最优模型(VIC-GOM)[76]则进一步探索了整合线性混合模型重构误差与体积不变约束的最优解,该方法可进一步对传统算法的端元获取精度进行优化. ...
Multispectral and Hyperspectral Image Analysis with Convex Cones
1
1999
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
Application of Convex Cone Analysis to Hyperspectral and Multispectral Scenes
1
2003
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
The Sequential Maximum Angle Convex Cone (SMACC) Endmember Model
1
2004
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
一种多/高光谱遥感图像端元提取的凸锥分析算法
1
2007
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
一种多/高光谱遥感图像端元提取的凸锥分析算法
1
2007
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
以凸面单体边界为搜索空间的端元快速提取算法
1
2010
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
以凸面单体边界为搜索空间的端元快速提取算法
1
2010
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
The Gamma Algorithm in Convex Cone Analysis of Hyperspectral Images
1
2009
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
Convex Cone-based Endmember Extraction for Hyperspectral Imagery
1
2010
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
Geometric Convex Cone Volume Analysis
1
2016
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
1
2016
... 相较正交投影、单形体体积类光谱解混方法,凸锥分析(Convex Cone Analysis,CCA)方法以高光谱图像各像元非负辐亮度物理特性为基础,通过寻找所有像元形成凸集的边缘或顶点来实现光谱解混[77].以此为基础,有学者基于凸锥原理,采用改进的施密特正交分解法来获取端元[78],并根据像元向量与凸锥的角度关系提出了顺序最大角凸锥端元提取算法[79];同期,国内也有学者提出了自动的CCA [80]以及基于凸体边界搜索[81]的端元提取方法;而Gamma算法的引入,可有效实现CCA端元提取中线性不等式组的计算[82];CCA与N-FINDR结合可减小CCA端元提取方法的计算复杂度[83];最近提出的凸锥体积分析(Convex Cone Volume Analysis, CCVA)和几何凸锥体积分析(Geometric CCVA, GCCVA)[84-85]通过将凸锥边缘向量向超平面的投影来减小图像背景信号对光谱解混的影响,同时也搭建了CCA与单形体体积求解的桥梁,简化了CCA方法的计算复杂度. ...
一种基于单形体正化的高光谱数据全约束线性解混方法
1
2016
... 可以看出,近30 a来,凸体几何类光谱解混方法的发展主要体现在两个方向,一是对高光谱图像在高维特征空间几何结构模型的优化,以线性混合模型为基础,加以ANC、ASC等不同的约束条件,构造光谱解混数学模型,出现了投影、凸锥和单形体体积等不同类型的光谱解混方法;二是在算法层面对计算效率和精度的优化,从端元矩阵行列式计算到矩阵三角分解、辅助高、单形体高、单形体正化[86]等的计算简化,以及在端元获取和丰度估计方面通过光谱解混模型的优化[87]来提升精度. ...
一种基于单形体正化的高光谱数据全约束线性解混方法
1
2016
... 可以看出,近30 a来,凸体几何类光谱解混方法的发展主要体现在两个方向,一是对高光谱图像在高维特征空间几何结构模型的优化,以线性混合模型为基础,加以ANC、ASC等不同的约束条件,构造光谱解混数学模型,出现了投影、凸锥和单形体体积等不同类型的光谱解混方法;二是在算法层面对计算效率和精度的优化,从端元矩阵行列式计算到矩阵三角分解、辅助高、单形体高、单形体正化[86]等的计算简化,以及在端元获取和丰度估计方面通过光谱解混模型的优化[87]来提升精度. ...
Statistical Volume Analysis: A New Endmember Extraction Method for Multi-hyperspectral Imagery
2
2016
... 可以看出,近30 a来,凸体几何类光谱解混方法的发展主要体现在两个方向,一是对高光谱图像在高维特征空间几何结构模型的优化,以线性混合模型为基础,加以ANC、ASC等不同的约束条件,构造光谱解混数学模型,出现了投影、凸锥和单形体体积等不同类型的光谱解混方法;二是在算法层面对计算效率和精度的优化,从端元矩阵行列式计算到矩阵三角分解、辅助高、单形体高、单形体正化[86]等的计算简化,以及在端元获取和丰度估计方面通过光谱解混模型的优化[87]来提升精度. ...
... 对于以图像中纯像元是否存在来划分的这两大类光谱解混方法,从计算量和算法意义的角度来看,满足纯像元存在假设类方法只需进行单形体体积计算和比较,其物理意义明确,因此相较后者具有计算量小、算法优化设计多等优点[2],但是在实际应用中,多数场景纯像元假设条件难以满足,会影响端元提取的精度;而后者则从图像中估计端元矩阵,适用于更多的场景,但需要采用优化方法对目标函数进行迭代求解,导致这类算法计算量偏大.同时,无论是端元提取还是端元生成方法,均容易受到图像噪声、异常点的影响,所幸已有方法[87,90]针对这类问题进行了探索,但由于噪声在真实数据中的广泛存在,这类克服噪声等干扰信息的方法还需进一步深入研究. ...
Fully Constrained Least Squares Linear Mixture Analysis for Material Quantification in Hyperspectral Imagery
1
2001
... 从另一个角度—图像中纯像元存在假设,也可对凸体几何类端元获取方法进行划分,后续的丰度估计可采用最小二乘法[88]或凸体几何关系来求解[72].满足纯像元存在假设类方法以图像中至少存在一个纯像元为前提,通过高光谱图像的凸体几何结构特征分析,从图像中获取存在的纯像元,因此这类方法被称为端元提取,典型的方法有PPI、N-FINDR、SGA、CCVA及其优化方法等;而无需纯像元假设的算法适用于更多的场景,其通过建立凸体结构目标函数优化模型并求解来获取虚拟端元[89],这些端元是对图像中纯像元的估计,因此这类方法常被称为端元生成方法,典型的方法有MVES、MVSA等. ...
A Quantitative Analysis of Virtual Endmembers' Increased Impact on the Collinearity Effect in Spectral Unmixing
1
2011
... 从另一个角度—图像中纯像元存在假设,也可对凸体几何类端元获取方法进行划分,后续的丰度估计可采用最小二乘法[88]或凸体几何关系来求解[72].满足纯像元存在假设类方法以图像中至少存在一个纯像元为前提,通过高光谱图像的凸体几何结构特征分析,从图像中获取存在的纯像元,因此这类方法被称为端元提取,典型的方法有PPI、N-FINDR、SGA、CCVA及其优化方法等;而无需纯像元假设的算法适用于更多的场景,其通过建立凸体结构目标函数优化模型并求解来获取虚拟端元[89],这些端元是对图像中纯像元的估计,因此这类方法常被称为端元生成方法,典型的方法有MVES、MVSA等. ...
A Simplex Volume Maximization Framework for Hyperspectral Endmember Extraction
1
2011
... 对于以图像中纯像元是否存在来划分的这两大类光谱解混方法,从计算量和算法意义的角度来看,满足纯像元存在假设类方法只需进行单形体体积计算和比较,其物理意义明确,因此相较后者具有计算量小、算法优化设计多等优点[2],但是在实际应用中,多数场景纯像元假设条件难以满足,会影响端元提取的精度;而后者则从图像中估计端元矩阵,适用于更多的场景,但需要采用优化方法对目标函数进行迭代求解,导致这类算法计算量偏大.同时,无论是端元提取还是端元生成方法,均容易受到图像噪声、异常点的影响,所幸已有方法[87,90]针对这类问题进行了探索,但由于噪声在真实数据中的广泛存在,这类克服噪声等干扰信息的方法还需进一步深入研究. ...
Information Extraction, SNR Improvement, and Data Compression in Multispectral Imagery
1
1973
... 数据降维处理在高光谱图像处理过程中可降低计算开销,同时也可满足N-FINDR、SGA等经典算法利用行列式进行单形体体积计算时的方阵所需,是一种经常被采用的高光谱图像处理方法.典型的数据降维方法主要有主成分分析(PCA)[91]、最大噪声分离(MNF)[92]等.通常情况下,数据降维处理会造成一些小目标信息的损失[93],但是,也有学者认为数据降维可提升端元提取算法的性能[26].针对不同噪声条件下数据降维对凸体几何类端元提取方法的影响,本文采用模拟数据对3种比较典型的端元提取方法ATGP(投影)、N-FINDR(体积)以及CCVA(凸锥)进行验证.模拟数据采用公式(1)生成: ...
A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal
1
1988
... 数据降维处理在高光谱图像处理过程中可降低计算开销,同时也可满足N-FINDR、SGA等经典算法利用行列式进行单形体体积计算时的方阵所需,是一种经常被采用的高光谱图像处理方法.典型的数据降维方法主要有主成分分析(PCA)[91]、最大噪声分离(MNF)[92]等.通常情况下,数据降维处理会造成一些小目标信息的损失[93],但是,也有学者认为数据降维可提升端元提取算法的性能[26].针对不同噪声条件下数据降维对凸体几何类端元提取方法的影响,本文采用模拟数据对3种比较典型的端元提取方法ATGP(投影)、N-FINDR(体积)以及CCVA(凸锥)进行验证.模拟数据采用公式(1)生成: ...
高光谱遥感图像目标探测与分类技术研究
2
2005
... 数据降维处理在高光谱图像处理过程中可降低计算开销,同时也可满足N-FINDR、SGA等经典算法利用行列式进行单形体体积计算时的方阵所需,是一种经常被采用的高光谱图像处理方法.典型的数据降维方法主要有主成分分析(PCA)[91]、最大噪声分离(MNF)[92]等.通常情况下,数据降维处理会造成一些小目标信息的损失[93],但是,也有学者认为数据降维可提升端元提取算法的性能[26].针对不同噪声条件下数据降维对凸体几何类端元提取方法的影响,本文采用模拟数据对3种比较典型的端元提取方法ATGP(投影)、N-FINDR(体积)以及CCVA(凸锥)进行验证.模拟数据采用公式(1)生成: ...
... 其中:n为端元数,表示行列式计算,为降维后的端元向量.公式(2)中行列式求解需要方阵,因此需要在行列式计算前进行高光谱数据的降维处理.为实现在原始数据空间计算单形体体积,减少数据降维处理对一些小目标信息的影响[93],出现了一种新的体积计算公式[95]: ...
高光谱遥感图像目标探测与分类技术研究
2
2005
... 数据降维处理在高光谱图像处理过程中可降低计算开销,同时也可满足N-FINDR、SGA等经典算法利用行列式进行单形体体积计算时的方阵所需,是一种经常被采用的高光谱图像处理方法.典型的数据降维方法主要有主成分分析(PCA)[91]、最大噪声分离(MNF)[92]等.通常情况下,数据降维处理会造成一些小目标信息的损失[93],但是,也有学者认为数据降维可提升端元提取算法的性能[26].针对不同噪声条件下数据降维对凸体几何类端元提取方法的影响,本文采用模拟数据对3种比较典型的端元提取方法ATGP(投影)、N-FINDR(体积)以及CCVA(凸锥)进行验证.模拟数据采用公式(1)生成: ...
... 其中:n为端元数,表示行列式计算,为降维后的端元向量.公式(2)中行列式求解需要方阵,因此需要在行列式计算前进行高光谱数据的降维处理.为实现在原始数据空间计算单形体体积,减少数据降维处理对一些小目标信息的影响[93],出现了一种新的体积计算公式[95]: ...
Identifiability of the Simplex Volume Minimization Criterion for Blind Hyperspectral Unmixing-The No-Pure-Pixel Case
1
2015
... 从实验结果可看出,最大体积标准获得的端元是模拟数据中存在的数据点,而最小体积包裹标准获得的是虚拟端元,其在实际数据点中并不存在.在噪声满足高斯分布且纯像元存在的条件下,从不同信噪比实验数据结果可以看出,最大体积标准获得的端元更接近真实端元.而在无纯像元条件下,有学者已经通过数值模拟结果表明,最小体积包裹标准可获得更鲁棒的端元估计[94]. ...
A New Volume Formula for a Simplex and Its Application to Endmember Extraction for Hyperspectral Image Analysis
2
2010
... 其中:n为端元数,表示行列式计算,为降维后的端元向量.公式(2)中行列式求解需要方阵,因此需要在行列式计算前进行高光谱数据的降维处理.为实现在原始数据空间计算单形体体积,减少数据降维处理对一些小目标信息的影响[93],出现了一种新的体积计算公式[95]: ...
... 该公式与公式(2)等价[95],式中表示光谱向量与初始化端元光谱向量的差值构成的矩阵,为矩阵转置. ...