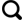1 前 言
陆表温度(Land Surface Temperature,LST)是指陆地表面的温度,在地-气相互作用过程中扮演着十分重要的角色,是全球变化研究的关键参数,对水文、生态、环境和生物地球化学等研究有重要意义。遥感越来越成为陆表温度观测的重要手段,但是由于n个通道的红外遥感观测只能建立n个方程,而未知数却有n+1个(n个Land Surface Emissivity(LSE),1个LST),方程组不完备,所以遥感陆表温度的反演具有不确定性[1],没有一定的先验知识,不可能同时反演得到LST与LSE。正是对先验知识假设的不同,不同学者发展了不同的陆表温度反演模型。主要分为LSE、LST同步反演的方法和已知LSE反演LST的方法[1]。应用广泛的分裂窗算法属于后者。
分裂窗(Split Window,SW)算法起源于20世纪70年代,最初用来确定海水表面温度[2]。Price首次将其推广到NOAA 7 AVHRR陆表温度的反演,将地表看做黑体,只考虑大气中水汽的吸收和辐射,算法的精度有很强的区域依赖性[3]。随后发展了多种不同的考虑大气和下垫面特征影响的陆表温度分裂窗反演算法。但多数研究均是基于热红外辐射传输方程,从理论的角度模拟分析的。如Becker等[4]通过利用辐射传输模式进行辐射亮温计算,结合地表实测数据,分析了不同大气状况下,地表发射率、温度对NOAA 9 AVHRR 4、5通道辐射亮温的影响。Sobrino等[5]则在参考Becker和Li工作的基础上,考虑了分裂窗通道地表比辐射率的影响。Coll等[6]将Plank函数引入辐射传输方程,并引入地表比辐射率对地表温度进行修正。Franca等[7]则不仅考虑了地表比辐射率、大气吸收系数以及大气水汽含量的影响,还考虑了大气透过率随观测角的变化。Wan-Dozier等[8]发展了广义分裂窗算法,对于已知地表比辐射率的表面,其精度可优于1 K,是目前广泛应用的MODIS地表温度产品所采用的算法。Yu等[9]针对GOES的实验也表明,LST对LSE非常敏感,尤其是白天,即使LSE较小的不准确性,也会给LST的反演带来较大的偏差,甚至高达3 K。陈瀚阅等[10]利用辐射传输模型MODTRAN 4.0以TIGR中纬度夏季廓线作为输入,基于Wan及Dozier分裂窗算法,研究大气水汽含量、地表比辐射率、通道等效噪声等参数的不确定度对反演精度的影响。结果表明,影响算法总精度的因素主要是算法绝对精度和地表比辐射率不确定度。
2 数据源及研究区
热红外遥感数据为Himawari 8 AHI分裂窗通道(中心波长分别为10.4 μm和12.4 μm)的数据。Himawari 8是日本2014年10月发射的新一代静止气象卫星,具有16个通道。本文所采用的数据获取于2016年6月17日,空间分辨率2 km,时间分辨率10 min,时间覆盖范围为世界时6:50至23:40。
陆表温度反演输入的陆表比辐射率是美国GORS-R ABI LST/LSE团队基于绿色植被覆盖度(Green Vegetation Fraction,GVF)开发的,反演所采用的算法具有较高的精度,裸地地区准确度达0.006[13]。
研究区选择了澳大利亚地区,Himawari对其有较好的覆盖,而且2016年6月17日晴空条件较好。
3 方 法
3.1 分裂窗算法
陆表温度反演采用Wan-Dozier的广义分裂窗算法,具体形式如下[8]:
其中:
3.2 陆表比辐射率误差噪声
为了评估陆表比辐射对陆表温度反演的影响,对所采用的陆表比辐射率产品分别加入不同的高斯分布噪声。图1显示了分别加入的3种不同的高斯噪声,均值分别为0.008、0.005和0.002,标准差分别为0.01、0.02和0.03,以此代表陆表比辐射率不同的误差水平,在后文中分别用噪声1、噪声2和噪声3表示。在其他输入相同的情况下,通过将带不同噪声的陆表比辐射率和原始的陆表比辐射率分别输入分裂窗算法,得到不同的陆表温度反演结果,通过陆表温度之间的差值,分析陆表比辐射对陆表温度反演结果的影响。
图1
图1
陆表比辐射率所添加的3种不同的高斯噪声
Fig.1
Three kind of noise added to the land surface emissivity
4 实验结果与分析
4.1 不同时间
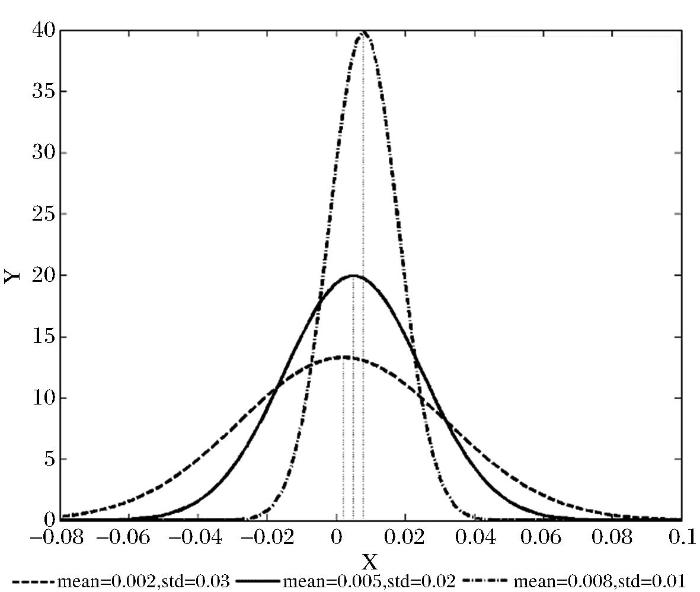
以世界时0700时和1600时分别代表研究区的白天和夜间,图2显示了白天、夜间与每日输入添加不同噪声的LSE与输入原始LSE所得的LST差值直方图。可以看出,白天、夜间和日均的共同特征为:输入添加噪声的LSE较输入原始的LSE反演的陆表温度数值总体略低,而且随着所添加噪声标准差的增大,所得LST差值的标准差增大。当LSE的噪声标准差为0.01时,所得白天、夜间和日均LST差值的标准差分别为0.48 K、0.52 K和0.34 K;而当LSE的噪声标准差为0.03时,所得LST差值的标准差分别为1.46 K、1.57 K和0.88 K。
图2
图2
不同时间输入添加不同噪声的LSE与输入原始LSE所得的LST差值直方图
Fig.2
The histogram of the LST difference retrieved from LSE with and without noise at different time
4.2 不同水汽条件
为分析不同水汽条件下陆表温度反演结果对陆表比辐射率的敏感性,将总的大气可降水分为1.5~3.0 g/cm2和3.0~4.5 g/cm2两组,分别反演并统计不同水汽条件下,输入带噪声的陆表比辐射率和输入原始陆表比辐射率反演所得的陆表温度。主要统计特征及结果如图3所示。
图3
图3
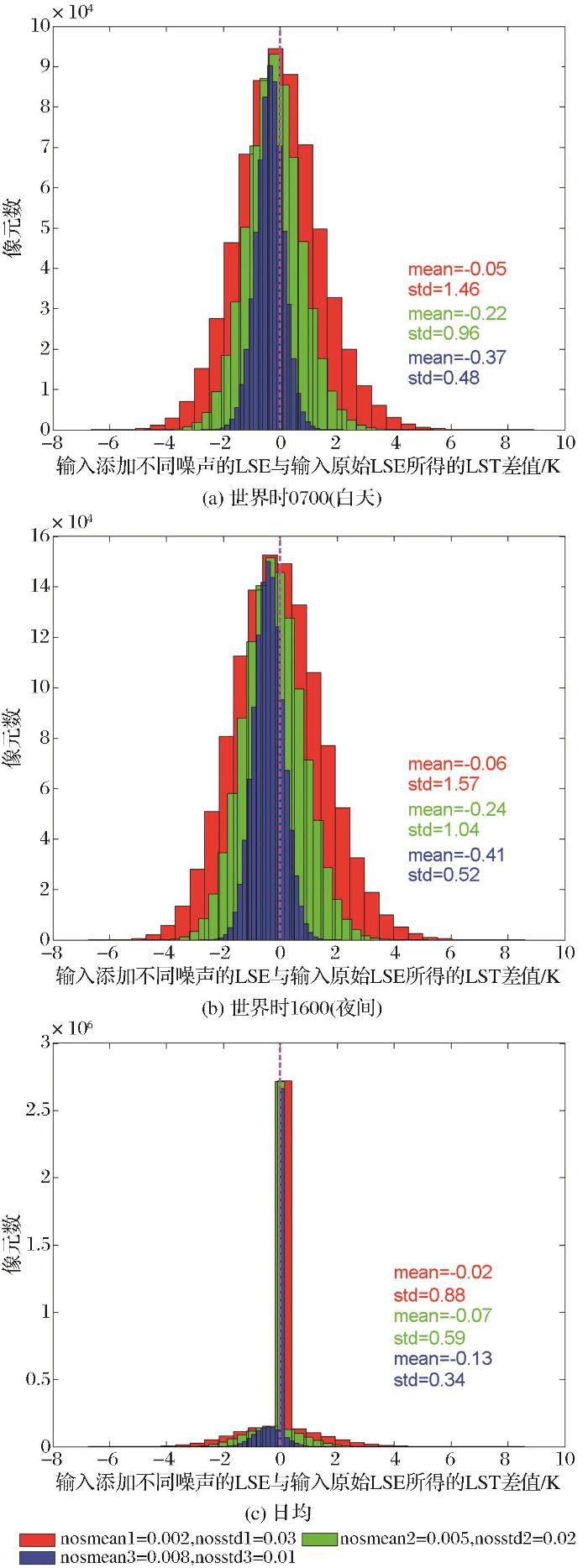
不同水汽条件下、不同时间输入添加不同噪声的LSE与输入原始LSE所得的LST统计特征
Fig.3
Statistics of LST retrieved from LSE with and without noise under different water vapor and time conditions
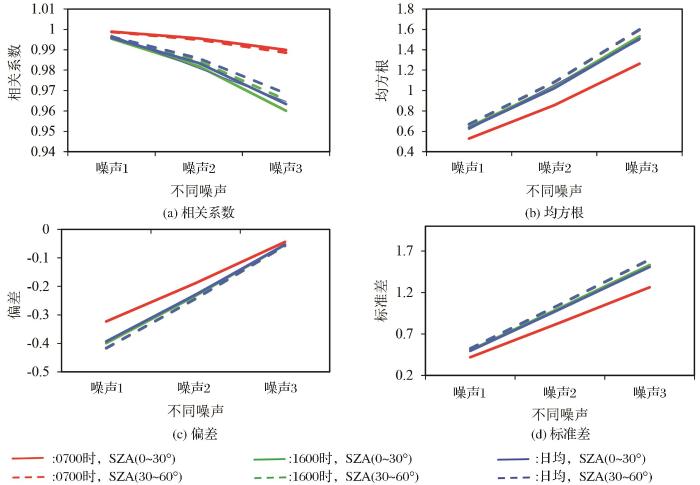
从图3所示的不同水汽条件下、不同时间输入添加不同噪声的LSE与输入原始LSE所得的LST统计特征可以看出,不管水汽条件如何,总体上,输入加入噪声的与输入原始陆表比辐射率反演所得的陆表温度相关系数随着所加噪声标准差的增大而减小,均方根误差和标准差随着所加噪声标准差的增大而增大,偏差为负值,其绝对值随着所加噪声标准差的增大而减小。在总的大气可降水处于1.5~3.0 g/cm2条件下,当LSE的噪声标准差为0.01时,所得白天、夜间和日均LST相关系数均为1.00,均方根误差分别为0.67 K、0.66 K和0.65 K,偏差分别为-0.42 K、-0.41 K、-0.41 K,标准差分别为0.53 K、0.52 K、0.51 K。而当LSE的噪声标准差为0.03时,所得白天、夜间和日均LST相关系数分别为0.99、0.98和0.98,均方根误差分别为1.60 K、1.57 K、1.56 K,偏差均为-0.06 K,标准差分别为1.60 K、1.57 K、1.56 K。在总的大气可降水处于3.0~4.5 g/cm2条件下,当LSE的噪声标准差为0.01时,所得白天、夜间和日均LST相关系数均为1.00,均方根误差分别为0.52 K、0.67 K和0.66 K,偏差分别为-0.32 K、-0.41 K、-0.41 K,标准差分别为0.41 K、0.52 K、0.52 K。而当LSE的噪声标准差为0.03时,所得白天、夜间和日均LST相关系数分别为0.99、0.95和0.97,均方根误差分别为1.23 K、1.59 K、1.57 K,偏差分别为-0.04 K、-0.06 K、-0.05 K,标准差分别为1.23 K、1.59 K、1.57 K。从以上的数值对比还可以看出,白天(07:00时)水汽较大时的相关系数大于水汽较小时;晚上(16:00时)和日均的相关系数则呈现相反的变化特征;相同的水汽变化条件下,白天两者的相关系数大于日均的,日均的大于晚上的。平方根误差、偏差和标准差只有白天水汽大的条件下与其他条件下数值差别较大,其几个条件下同一统计特征数值十分接近。其中,均方根误差和标准差,白天水汽大的条件下较其他条件下数值小,而偏差绝对值也较小 。
4.3 不同角度条件
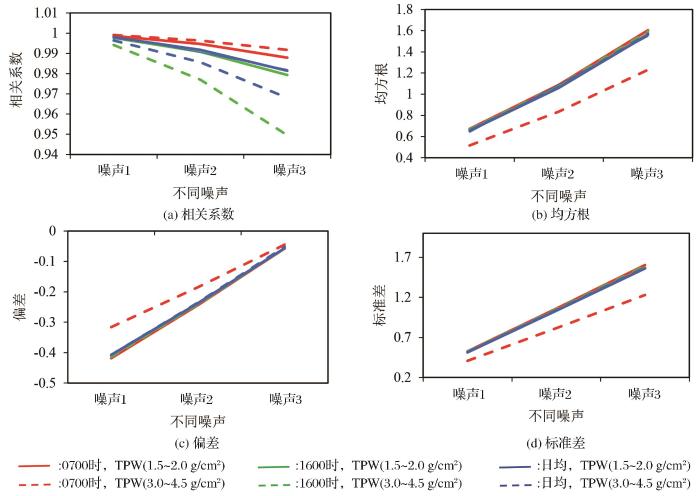
从图4所示的不同角度条件下、不同时间输入添加不同噪声的LSE与输入原始LSE所得的LST统计特征可以看出,不管角度条件如何,总体上,输入加入噪声的与输入原始陆表比辐射率反演所得的陆表温度相关系数随着所加噪声标准差的增大而减小,均方根误差和标准差随着所加噪声标准差的增大而增大偏差为负值,其绝对值随着所加噪声标准差的增大而减小。在卫星天顶角0~30°条件下,当LSE的噪声标准差为0.01时,所得白天、夜间和日均LST相关系数均为1.00,均方根误差分别为0.53 K、0.64 K和0.63 K,偏差分别为-0.32 K、-0.40 K、-0.39 K,标准差分别为0.42 K、0.50 K、0.50 K。而当LSE的噪声标准差为0.03时,所得白天、夜间和日均LST相关系数分别为0.99、0.96和0.96,均方根误差分别为1.26 K、1.53 K、1.51 K,偏差分别为-0.04 K、-0.05 K、-0.05 K,标准差分别为1.26 K、1.53 K、1.51 K。在卫星天顶角30~60°条件下,当LSE的噪声标准差为0.01时,所得白天、夜间和日均LST相关系数均为1.00,均方根误差均为0.67 K,偏差均为-0.42 K,标准差分别为0.52 K、0.53 K、0.52 K。而当LSE的噪声标准差为0.03时,所得白天、夜间和日均LST相关系数分别为0.99、0.97和0.97,均方根误差均为1.60 K,偏差均为-0.06 K,标准差分别为1.59 K、1.60 K、1.60 K。从以上的数值对比还可以看出,白天(07:00时)角度较小时的相关系数略大于角度较大时;晚上(16:00时)和日均的相关系数则呈现相反的变化特征;相同的角度变化条件下,白天的相关系数大于日均的大于晚上的。均方根误差、偏差和标准差只有白天角度小的条件下与其他条件下数值差别较大,其他几个条件下同一统计特征数值比较接近。其中,均方根误差和标准差,白天角度的条件下较其它条件下数值小,而偏差则较大。
图4
图4
不同角度条件下、不同时间输入添加不同噪声的LSE与输入原始LSE所得的LST统计特征
Fig.4
Statistics of LST retrieved from LSE with and without noise under different sensor zenith angle and time conditions
4.4 不同下垫面类型
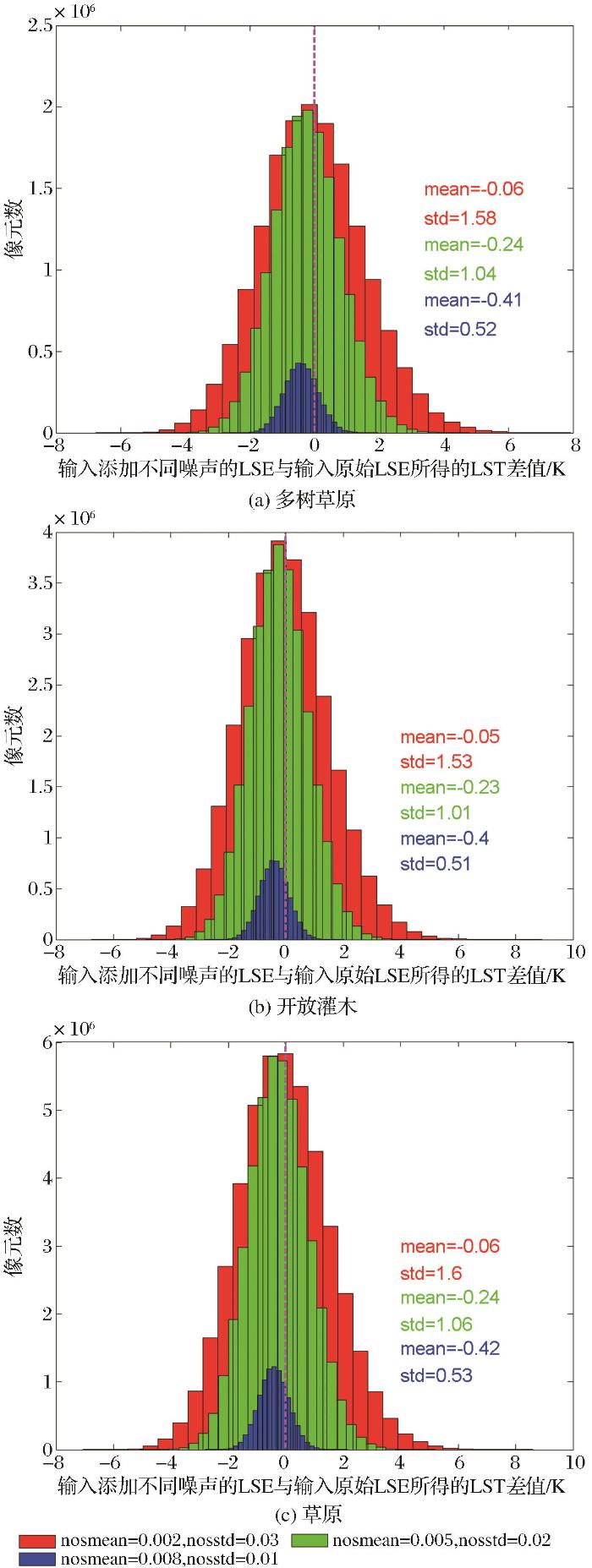
选择了研究区3种典型的下垫面类型:多树草原(Woody savannas)、开放灌木(Open shrubland)和草原(Savannas),分析不同下垫面条件下输入添加不同噪声的LSE与输入原始LSE所得的LST的差异,结果如图5所示。可以看出,对于不同的下垫面,随着所加噪声标准差的增大,LST差值的标准差增大,当所加噪声标准差为0.01时,多树草原、开放灌木和草原LST差值的标准差分别为0.52 K、0.51 K和0.53 K。当所加噪声标准差为0.03时,三者LST差值的标准差分别为1.58 K、1.53 K和1.6 K。也就是当LSE添加相同的噪声时,草原LST差值的标准差略大于木质草原的,而木质草原的大于开放灌木的。
图5
图5
不同下垫面条件下输入添加不同噪声的LSE与输入原始LSE所得的LST差值散点图
Fig.5
The histogram of LST difference retrieved from LSE with and without noise under different land surface types
5 结 论
为探讨红外遥感陆表温度反演过程中,陆表比辐射率对反演结果的影响,本文基于Himawari 8 AHI (Advanced Himawari Imager, AHI)的分裂窗通道热红外遥感数据和Wan 及Dozier分裂窗算法,通过对陆表比辐射率产品分别加入不同均值和标准差的高斯分布噪声,以此代表陆表比辐射率不同的误差水平;分析不同时间、不同水汽、不同观测角度和不同下垫面条件下,陆表温度对陆表比辐射率的敏感性。主要结论如下:
(1)不论白天、夜间还是日均LST,输入添加噪声的LSE较输入原始的LSE反演所得的陆表温度数值总体略低,而且随着所添加噪声标准差的增大,所得LST差值的标准差增大。当输入LSE的噪声标准差为0.01时,所得白天、夜间和日均LST与输入不添加噪声的LSE所得的LST差值的标准差分别为0.48 K、0.52 K和0.34 K;而当LSE的噪声标准差为0.03时,两者差值的标准差则分别升高到1.46 K、1.57 K和0.88 K。
(2)不管水汽和观测角度条件如何,总体上,输入加入噪声的与输入原始LSE反演所得的LST相关系数随着所加噪声标准差的增大而减小,均方根误差和标准差随着所加噪声标准差的增大而增大,而偏差为负值,其绝对值随着所加噪声标准差的增大而减小。
(3)对于不同的下垫面,随着所加噪声标准差的增大,LST差值的标准差增大,其中,草原(Savannas)的标准差略大于多树草原(Woody savannas)的,而多树草原的大于开放灌木(Open shrubland)的。 当LSE所加噪声标准差为0.01时,反演所得多树草原、开放灌木和草原LST与输入不带噪声的LSE所得LST差值的标准差分别为0.52 K、0.51 K和0.53 K。而当LSE所加噪声标准差为0.03时,LST差值的标准差分别升高到1.58 K、1.53 K和1.6 K。
本文研究不仅有助于遥感陆表温度反演过程中LSE数据源的选择,而且有助于遥感LST反演结果的分析和理解。
参考文献
Satellite-derived land surface temperature: Current status and perspectives
[J].
Estimation of sea surface temperatures from space
[J].
Land surface temperature measurements from split window channels of the NOAA 7 advance very high resolution radiometer
[J].
Toward a local split window method over land surface
[J].
A methodology for obtaining the crop temperature from NOAA-9 AVHRR data
[J].
On the atmospheric dependence of the split-window equation for land temperature
[J].
Retrieval of land and sea surface temperature using NOAA-11 AVHRR data in north-eastern Brazill
[J].
A generalized split-window algorithm for retrieving land- surface temperature from space
[J].
Developing algo-rithm for operational GOES-R land surface temperature product
[J].
Comparison of LST retrieval precision and sensitivity analysis between two split-window algorithems
[D].
劈窗算法陆表温度反演精度比较与敏感性分析
[D].
Evaluation of split-window land surface temperature algorithms for generating climate data records
[J].
Optimization of vegetation emissivity scheme and Land Surface Temperature simulation over the Tibetan Plateau in CLM
[D].
CLM中植被发射率方案的发展及其对青藏高原地表温度的模拟
[D].
Land surface emissivity product for NOAA JPSS and GOES-R missions: Methodology and evaluation
[J].