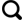星载多普勒雷达云中大气风场测量仿真研究

doi:10.11873/j.issn.1004-0323.2023.4.0903

星载多普勒雷达云中大气风场测量仿真研究

刘顺飞^,¹^,², 朱迪¹, 董晓龙^,¹^,²

1.中国科学院国家空间科学中心，北京 101400

2.中国科学院大学，北京 100049

Study and Simulation on Measurement of Atmospheric Wind Field in Cloud by Spaceborne Doppler Radar

LIU Shunfei^,¹^,², ZHU Di¹, DONG Xiaolong^,¹^,²

1.National Space Science Center，Chinese Academy of Sciences，Beijing 101400，China

2.University of Chinese Academy of Sciences，Beijing 100049，China

通讯作者: 董晓龙（1969-），男，陕西大荔人，博士生导师，研究员,主要从事新型微波遥感探测与成像及微波遥感信息获取的方法与技术研究。E⁃mail: dongxiaolong@mirslab.cn

收稿日期: 2022-03-10 修回日期: 2023-04-24

基金资助:

空间科学预先研究项目“星载毫米波云雷达多普勒信号探测技术研究”. XDA15018600
空间科学预先研究项目“星载毫米波云雷达多普勒信号探测技术研究”. XDA15018600

Received: 2022-03-10 Revised: 2023-04-24

作者简介 About authors

刘顺飞（1997-），男，湖南邵阳人，硕士研究生，主要从事微波遥感探测等方面的研究E⁃mail:m15971270145@163.com , E-mail：m15971270145@163.com

摘要

全球风廓线的测量对提高数值天气预报精度，准确描述气候模型，理解大气中的物理过程具有重要意义。云雨条件下，星载大气风场多普勒速度测量能力依赖于雷达系统参数、云的物理和动力特征及测量方法。基于极化分集脉冲对（Polarization Diversity Pulse-Pair， PDPP）算法，研究了脉冲时序和多普勒速度测量精度的关系。对影响PDPP方法多普勒测量精度的因素进行了仿真分析。结果表明，对W波段雷达，脉冲对重复频率应当在3.5~5 KHz范围。使用0.1°波束宽度的天线在脉冲间隔为30~50 us区间内，能对反射率因子-20 dBZ的云内风速进行测量，精度在1.35 m/s；相同精度要求下，0.2°波束宽度的天线在脉冲间隔为30~40 us范围内，能达到探测灵敏度约-12 dBZ。

关键词： 云内大气风场 ; 极化分集脉冲对算法 ; PRF设计 ; 多普勒测量

Abstract

Global wind profile plays a critical role in improving accuracy of numerical weather prediction， accurately describing climate models and understanding the atmospheric physical processes. Under cloud and rain conditions， the Doppler velocity measurement ability of spaceborne atmospheric wind field is highly dependent on radar system parameters， the physical and dynamic characteristics of cloud and measurement method. Based on Polarization Diversity Pulse Pair （PDPP） algorithm， the relationship between pulse timing and Doppler velocity measurement accuracy is studied. The factors affecting the Doppler measurement accuracy of PDPP method are simulated and analyzed. The results show that for W-band radar， the pulse pair repetition frequency should be in the range of 3.5~5 kHz. The antenna with 0.1 ° beam width can measure the in-cloud wind speed with reflectivity factor of about -20dBz in the pulse interval of 30~50 μs， and the accuracy is 1.35 m/s； Under the same accuracy requirements， the antenna with 0.2° beam width can achieve detection sensitivity of about -12 dBz in the range of pulse interval of 30~40 μs.

Keywords： Atmospheric wind field in cloud ; Polarization diversity pulse pair algorithm ; PRF design ; Doppler measurement

PDF (5349KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘顺飞, 朱迪, 董晓龙. 星载多普勒雷达云中大气风场测量仿真研究. 遥感技术与应用[J], 2023, 38(4): 903-912 doi:10.11873/j.issn.1004-0323.2023.4.0903

LIU Shunfei, ZHU Di, DONG Xiaolong. Study and Simulation on Measurement of Atmospheric Wind Field in Cloud by Spaceborne Doppler Radar. Remote Sensing Technology and Application[J], 2023, 38(4): 903-912 doi:10.11873/j.issn.1004-0323.2023.4.0903

1 引言

大气风场是重要的气象要素，将三维风场的测量结果同化到天气预报模式中，改进数值天气预报（NWP）的初始条件，将显著提高预报精度。世界气象组织明确指出，全球风廓线“对于所有尺度和所有纬度的业务天气预报至关重要”^［1］。全球风场的精确测量也能帮助推动一些关键气候变化问题的研究。有研究表明，大气环流在10 a时间尺度上的改变，其中一些变化可能是受到温室气体的作用影响，而研究所依赖的气候模型和数据集并不能对大尺度环流的变化提供完整信息。由于热带大气的大部分地区没有实测的风廓线，考虑到风场在质量—运动平衡关系中的主导地位，风廓线测量对于热带气旋、季风环流和非洲东风急流等热带现象，其预测水平将会有很大的提升^［2］。高分辨率的全球大气风场数据是WMO迫切需要的，然而获取全球风场也面临许多挑战。

地基风廓线雷达是获取风场信息的重要手段，多雷达组网观测技术已经成熟，但该方法受到地形地貌限制，在海洋及偏远山地无法布设观测站，使得这些区域观测数据匮乏。星载微波散射计通过测量海面后向散射系数反演海表面风场，但不能用于陆地风场，且无法获得海洋上空的大气风场。云导风技术通过静止轨道气象卫星成像获得连续时序的卫星云图，捕捉云图上示踪云团的运动轨迹推算风速和风向，缺点在于无法获得云内部垂直尺度的对流特征。低轨卫星上使用大气目标（气溶胶，云雨粒子）作为风的“示踪物”的多普勒主动传感器（激光雷达和雷达）来进行全球风测量被认为是一种有效手段。2018年发射的欧空局风神任务提供了第一个多普勒激光雷达测量晴空和薄冰云中的视线风。McNally^［3］的研究表明，多云区域的风观测能提升预报潜力。星载多普勒激光测风雷达适用于晴空大气风场测量，但在面对云雨条件时，由于激光无法穿透云层，因而不能获取云内风的信息。ESA-JAXA EarthCARE任务通过天底点指向的W波段多普勒云雷达提供云粒子的垂直速度，首次实现从太空观测冰晶沉积速率、上升对流和下沉气流的能力，但该多普勒雷达无法在深云系统中提供水平风场^［4］。水平风的测量需要偏离天底点且具有多波束的立体雷达或具有扫描能力的多普勒雷达，通过对同一观测单元实现不同方位角的观测得到的径向速度估计来反演水平风分量。多普勒速度精度要求取决于应用，NWP对低对流层水平风的实现目标是误差小于2 ms^-1，水平分辨率15 km，垂直分辨率0.5 km^［1］。

实现星载云雷达多普勒径向速度的测量是反演三维风场的基础，云雨粒子对W波段频率的电磁波表现出明显的散射特性，而多普勒雷达通过测量随风运动的水凝物粒子的后向散射信号的多普勒频移，根据多普勒频移和径向速度的关系实现速度探测。多普勒频率的估计方法有基于DFT的谱分析方法，通过频谱的一阶矩和二阶矩得到平均频率和谱宽的估计，该方法需要在高采样率下进行频谱变换，运算较为复杂。星载多普勒雷达对多普勒频率的估计多采用时域的脉冲对算法（Pulse Pair Processing， PPP），通过发射脉冲对形式的信号，若探测目标存在径向运动，则接收到的一对脉冲信号会因多普勒频移在脉冲对间隔内的积累表现出相位差，利用相位差估计平均频移从而得到速度的估计，它可以直接在时域完成速度估计，处理上更为方便。其中，脉冲对间隔受最大无模糊距离和最大无模糊速度的约束。星载平台上的脉冲对操作相比地基或机载平台会面临更多的困难，因为卫星的高速运动引起的多普勒衰落使信号的去相关严重，而为了满足足够的探测范围（最大无模糊距离），对于0~20 km高度范围分布的云，接收窗长度至少为133.3 us，对应W波段电磁波测量的最大无模糊速度为6 m/s。在极端天气情况下，如台风飑线过境时常伴随短时间风向突变、风速增大情况，速度可能超过40 m/s，在这样的脉冲间隔下会产生速度模糊。为了增强风暴、强对流等气象条件下速度测量范围，Doviak等^［5］提出了极化分集脉冲对（Polarization Diversity Pulse-Pair，PDPP）算法，通过发射时间间隔更短的正交极化脉冲，用两个通道同时接收两个正交极化脉冲的后向散射信号，进一步减小脉冲间隔来提高最大无模糊速度。但PDPP方法也会存在交叉极化串扰效应等影响，其速度测量精度需结合脉冲对算法估计性能加以分析。

本文介绍了星载大气风场的探测原理和基于脉冲对的多普勒频率估计方法，分析了回波脉冲对去相关的因素，仿真了相关系数对观测俯仰角和方位角的依赖性，分析了脉冲对间隔、速度谱标准差、波束宽度、信噪比对速度测量精度的影响规律，优化了脉冲时序参数。

2 星载大气云内风场探测方法

目前对高空云内风场观测尚无有效手段，但可以通过测量受到风场影响的云雨粒子的运动速度间接反演风场。电磁波在大气传播的过程中，与大气中水凝物粒子相互作用产生后向散射回波，雷达的检测是基于具有一定信噪比的散射信号，对信号功率的测量能得到反射率因子强度的信息；而回波信号相位的改变与多普勒频移有关，通过平均多普勒频移能够得到云雨粒子在波束视轴上速度的估计，根据多方向径向速度结合观测几何可实现三维风场的反演。

2.1　基于脉冲对干涉的径向速度估计

雷达接收到回波信号由分辨体积单元内各个云粒子散射的电磁波叠加得到。由于每个云粒子具有不同的运动速度，在雷达波束照射方向投影后对应于不同的多普勒频移，使观测得到的频谱具有一定的谱宽。脉冲对算法（PPP）提供了对该分辨单元内平均径向速度的一种估计，将接收的相邻两脉冲做复相关，对相关函数的相位在脉冲重复周期 $T_{p r i}$ 内的平均作为多普勒频率的估计，最后根据多普勒频移和目标径向速度的关系：得到平均速度的估计。

f_{d} = \frac{2 v}{λ}

（1）

实际处理时，会采用多脉冲对累积的方法，提高频率估计精度。设第k个脉冲回波信号的时域表示为：

Z_{k} = |Z_{k}| e^{j (ω t + ϕ_{k})}

（2）

将其与第k+1个脉冲回波进行复相关：

{Z_{k}}^{*} Z_{k + 1} = |Z_{k} Z_{k + 1}| e^{j (ϕ_{k + 1} - ϕ_{k})}

（3）

对M组脉冲平均后，平均径向速度的估计为：

{\hat{v}}^{p p} = \frac{λ}{4 π T_{p r i}} a r g \frac{1}{M} \sum_{k = 0}^{M - 1} {Z_{k}}^{*} Z_{k + 1}

（4）

传统的脉冲发射时序如图1（a）所示，探测范围限制了PRF上界。这种脉冲时序无法解决最大无模糊速度 $V_{m a x}$ 和最大无模糊距离 $r_{m a x}$ 的两难。而极化分集脉冲对（PDPP）技术利用正交极化信号之间的隔离来防止回波重叠，同时通过大气粒子的正交同极化后向散射系数（ $S_{v v}$ 和 $S_{h h}$ ）之间的相关性来测量速度。图1（b）为Doviak和Sirmans提出的PDPP序列。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 传统脉冲对时序和PDPP脉冲时序对比

Fig.1 Comparison of Traditional Pulse Pair Timing and PDPP Pulse Timing

H和V通道中接收的复电压信号分别为 $V_{H}$ 和 $V_{V}$ ， v-h脉冲对和h-v脉冲对的相关函数分别记为 $R_{v h}$ ， $R_{h v}$ ，则M个样本累积后的相关函数为^［6］：τ

R_{v h} = \frac{1}{M} \sum V_{H} V_{V}^{*}

（5）

R_{h v} = \frac{1}{M} \sum V_{V} V_{H}^{*}

（6）

在PDPP方法估计中，相关信号的时间间隔为 $T_{v h}$ ，可得到平均速度的估计为：

{\hat{v}}^{m e a n} = \frac{λ}{4 π T_{v h}} a r c t a n (\frac{I m \{\sqrt[]{R_{v h} (T_{v h}) R_{h v} (T_{h v})}\}}{R e \{\sqrt[]{R_{v h} (T_{v h}) R_{h v} (T_{h v})}\}})

（7）

其中： $I m$ 表示虚部； $R e$ 表示实部。

2.2　风场矢量的建立

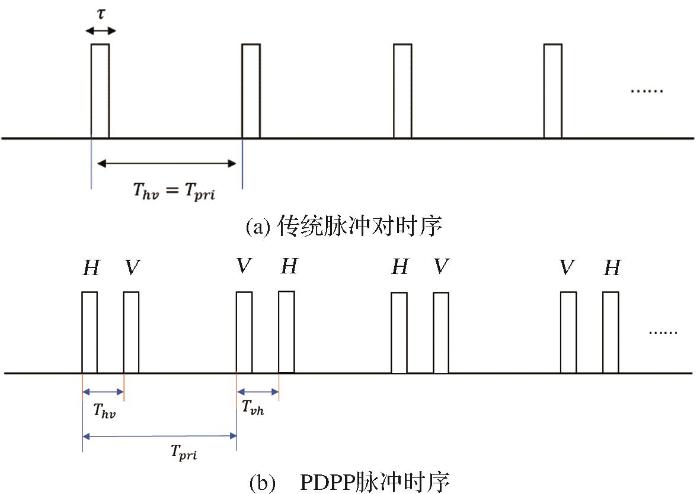
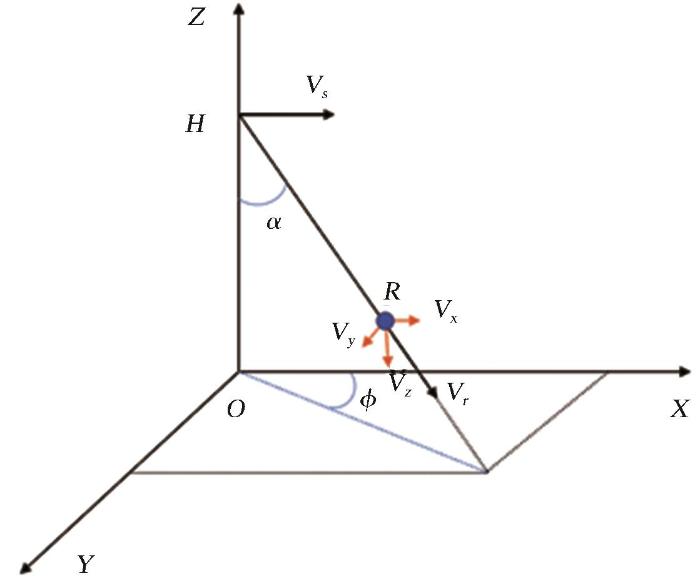
根据如下观测几何，卫星距离观测云层的垂直高度为 $H_{s}$ ，X轴指向卫星速度方向，Z轴指向天底。 $α_{1}$ 和 $α_{2}$ 分别是两个波束俯仰角。卫星运动时同一波束对刈幅宽度内的分辨单元可以得到前视和后视两次观测。因此内波束刈幅范围内的分辨单元一共可以获得4次不同方位上的观测。内外波束之间的体积分辨单元可以获得两次不同方位上的观测（图2）。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 实现三维风速反演的观测几何

Fig.2 Observation Geometry for Realizing 3D Wind Speed Inversion

测量得到的多普勒速度是相对于雷达在坐标处（R， $α$ ，φ）目标速度的径向分量：

v_{r} = (v_{x} - V_{s}) s i n α c o s φ + v_{y} s i n α s i n φ + v_{z} c o s α

（8）

具有两个不同俯仰角波束的雷达，对同一分辨单元在各波束上观测方位角不同，由3个不同观测方位测得的径向速度可得到该处的三维速度矢量：

(\begin{matrix} s i n α_{1} c o s φ_{1} & s i n α_{1} s i n φ_{1} & c o s α_{1} \\ s i n α_{2} c o s φ_{2} & s i n α_{2} s i n φ_{2} & c o s α_{2} \\ s i n α_{3} c o s φ_{3} & s i n α_{3} s i n φ_{3} & c o s α_{3} \end{matrix}) (\begin{matrix} v_{x} - V_{s} \\ v_{y} \\ v_{z} \end{matrix}) = (\begin{matrix} v_{r 1} \\ v_{r 2} \\ v_{r 3} \end{matrix})

（9）

解为：

(\begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix}) = {(\begin{matrix} s i n α_{1} c o s φ_{1} & s i n α_{1} s i n φ_{1} & c o s α_{1} \\ s i n α_{2} c o s φ_{2} & s i n α_{2} s i n φ_{2} & c o s α_{2} \\ s i n α_{3} c o s φ_{3} & s i n α_{3} s i n φ_{3} & c o s α_{3} \end{matrix})}^{- 1} (\begin{matrix} v_{r 1} \\ v_{r 2} \\ v_{r 3} \end{matrix}) + (\begin{matrix} V_{s} \\ 0 \\ 0 \end{matrix})

（10）

3 PDPP速度测量精度分析与仿真

雷达波束照射的体积单元内，假设各云粒子运动是随机的且相互独立，回波信号为每个粒子散射结果的非相干叠加。由中心极限定理，大量独立的随机变量之和满足高斯分布，即多普勒速度谱满足高斯分布，根据多普勒速度和多普勒频率的线性关系，其回波的功率谱具有如下形式^［8］：

S (f) = \frac{S}{\sqrt[]{2 π} σ_{f}} e x p [- \frac{{(f - \bar{f_{d}})}^{2}}{2 σ_{f}^{2}}] + N

S为信号功率， $\bar{f_{d}}$ 为平均多普勒频移， $σ_{f}$ 为多普勒谱标准差，N为噪声功率密度。对功率谱进行傅里叶反变换得到高斯谱的自相关函数。

R (τ) = S β (τ) e^{j 2 π \bar{f_{d}} τ} + N δ (τ)

其中：

β (τ) = e^{- 2 π^{2} σ_{f}^{2} τ^{2}}

$δ (τ)$ 是冲击函数，对于H极化和V极化脉冲对间隔 $T_{h v}$ ，脉冲重复间隔 $T_{p r i}$ 的极化分集脉冲对（PDPP）时序，不考虑交叉极化影响时，极化分集脉冲对算法的多普勒速度测量方差^［9］表示为：

v a r (v_{d}) = \frac{λ^{2}}{16 π^{2} {T_{h v}}^{2}} \times {\frac{1 - β^{2} (T_{h v})}{2 M^{2} β^{2} (T_{h v})} \sum_{m = - (M - 1)}^{M - 1} β^{2} (m T_{p r i}) (M - |m|) + \frac{N^{2}}{2 M S^{2} β^{2} (T_{h v})} + \frac{N}{M S β^{2} (T_{h v})} \times [1 + (1 - \frac{1}{M}) β (T_{h v}) μ (T_{p r i} - T_{h v})]}

其中：

μ (τ) = \{\begin{matrix} 1 τ = 0 \\ 0 τ \neq 0 \end{matrix}

从表达式中可以看出，气象目标的谱展宽影响回波信号的相关函数，大的谱宽会使信号零延时相关函数值减小，从而影响精度。影响速度估计精度的因素还有H⁃V脉冲间隔、脉冲对重复周期、信噪比、脉冲对累积数以及H⁃V脉冲之间的极化串扰效应。下面将分别进行讨论。

3.1　信噪比及其影响

信噪比会影响速度估计精度。天线接收波束采样体积内云粒子的后向散射信号，接收机输出的平均功率和云粒子对电磁波的散射特性有关。气象雷达方程描述了云的反射率因子强度和回波功率的关系。 $P_{t}$ 为雷达的发射功率，G是观测视轴上天线增益（收发同天线），L为系统损耗，k是衰减系数， $α 、 φ$ 分别为俯仰和方位向波束宽度， $|K|$ 与水的介电常数有关。c表示电磁波传输速度，τ是发射脉冲宽度；λ是雷达发射的电磁波波长；Z代表气象目标反射率因子，对距离 $r$ 处的云目标，接收到的回波功率 $P_{r}$ 为^［7］：

P_{r} = \frac{P_{t} G^{2} π^{3} α φ c τ {|K|}^{2}}{1024 (I n 2) L λ^{4} r^{2}} Z 10^{- 0.2 \int_{0}^{r} k d r}

（16）

反射率因子Z与云粒子的滴谱分布函数有关，对不同类型的云，其反射率因子存在差异，导致测量的回波功率不同，从而影响信噪比。对于降水云而言，其反射率因子可高于15 dBZ，而层积云或卷云等反射率因子通常在-20 dBZ以下。

雷达接收机的噪声功率可表示为：

P_{N} = N_{F} k_{B} T B

（17）

其中： $B$ 为接收机带宽； $T$ 为环境温度； $k_{B} = 1.380 6 \times 10^{- 23} J / K$ 为玻尔兹曼常数； $N_{F}$ 为接收机的噪声系数。系统信噪比可以表示为：

S N R = \frac{P_{r}}{P_{N}} = \frac{P_{t} G^{2} π^{3} α φ c τ {|K|}^{2}}{1024 (I n 2) L λ^{4} r^{2} N_{F} k_{B} T B} Z 10^{- 0.2 \int_{0}^{r} k d r}

（18）

在系统参数设计时，应考虑探测灵敏度的需求与系统信噪比的关系。仿真采用的雷达系统参数如表1所示。

表1 W波段雷达系统参数

Table 1 W-band radar system parameters

参数符号	说明	单位	数值
$λ$	波长	mm	3.2
$P_{t}$	发射峰值功率	W	1800
$τ$	脉冲宽度	μs	3.3
$Θ$	俯仰向波束宽度	°	0.1~0.2
$Φ$	方位向波束宽度	°	0.1~0.2
$F_{n}$	噪声系数	dB	5
B	接收带宽	MHz	0.36
T	绝对温度	K	290
L	系统损耗	dB	4

新窗口打开| 下载CSV

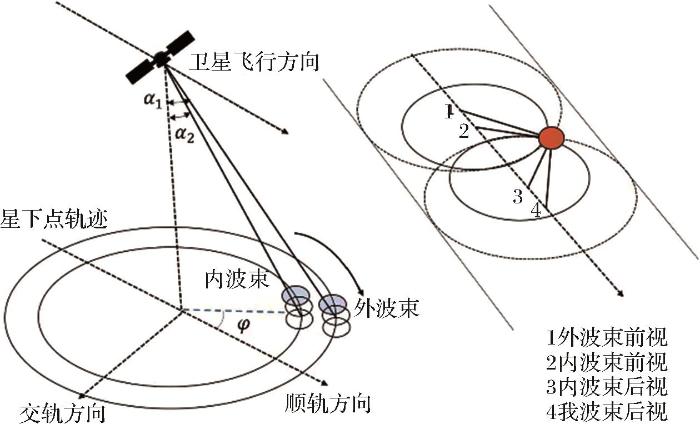
卫星的轨道高度为500 km，观测俯仰角为41°，云层高度距离地面100 m，在根据气象雷达方程，得到该系统参数下不同反射率因子对应的回波信噪比（图3）。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 回波信噪比与反射率因子关系

Fig.3 Relationship between echo signal-to-noise ratio and reflectivity factor

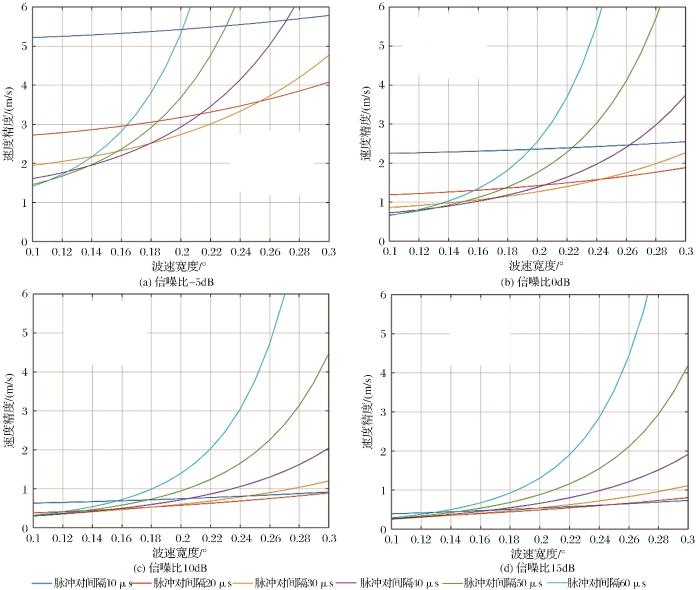
不同反射率因子对应的速度精度结果如图4所示，仿真气象条件参数选取依据表2，风速标准差1 m/s，云粒子下落速度的多普勒谱宽标准差为0.5 m/s，不考虑极化串扰影响，风切变常数为0.005 m/s，脉冲积累数为200，观测方位角90°，脉冲重复频率4 kHz。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 速度精度与反射率因子的关系

Fig.4 Relationship between velocity accuracy and reflectivity factor

表2 谱方差变化范围

Table 2 Variation range of spectral variance

参数(m²/s²)	方位角0°	方位角90°
${σ_{m o v e}}^{2}$	7.79	13.69
${σ_{r}}^{2}$	0.1~9.69	0.1~9.69
${σ_{v f o b}}^{2}$	0.25~1	0.25~1
${σ_{w s}}^{2}$	1~16	1~16
${σ_{t o t a l}}^{2}$	9.14~34.48	15.04~44.38

新窗口打开| 下载CSV

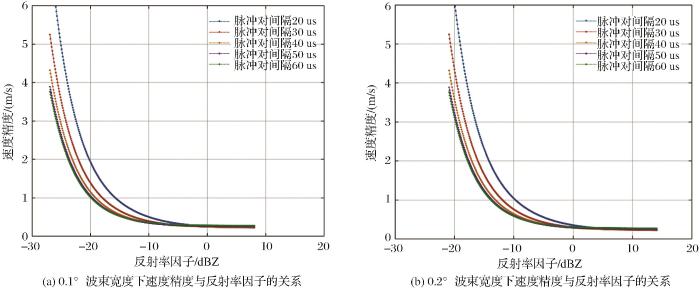
图4（a）、图4（b）分别为波束宽度为0.1°，0.2°条件的下速度测量精度的仿真结果。在相同的观测条件下，采用较窄的波束能减小分辨单元内回波信号的谱展宽，减小粒子运动产生的时间去相关；同时，对相同反射率强度的云，因增益更高从而使回波具有更大的信噪比，因而PDPP算法的速度估计精度更高。对于0.1°的波束宽度，若要求速度精度优于1.35 m/s，采用20 us的脉冲对间隔仅能探测反射率因子高于约-17 dBZ的云，而60 us的脉冲间隔可以使探测灵敏度提升到约-22 dBZ；使用0.2°波束宽度天线，在20 us脉冲间隔下其探测灵敏度约为-12 dBZ，采用60 us的脉冲间隔满足速度测量需求的反射率强度约为-16 dBZ。

3.2　相关函数中谱展宽影响

由于速度测量精度依赖于多普勒频率估计精度，而极化分集脉冲对算法利用相邻H-V脉冲的复相关函数的相位估计平均频率，因此脉冲对的相关性会影响速度精度。相关函数不仅与时间间隔有关，还受多普勒谱宽影响，大的谱宽会导致回波信号间的去相干，星载平台中导致多普勒谱展宽的因素有：天线波束视角内风切变引起的谱展宽 $σ_{r}$ ，卫星运动的多普勒衰落引起的谱展宽 $σ_{m o v e}$ ，大气湍流、风速方差引起的谱展宽 $σ_{w s}$ ，观测单元内云粒子下落引起的谱展宽 $σ_{v f o b}$ 。以下分析了引起多普勒速度谱展宽的因素。

对距离R处以速度 $(v_{x}, v_{y}, v_{z})$ 运动的云粒子，观测俯仰角为 $α$ ，方位角 $φ$ ，卫星轨道高度为H，其速度矢量沿X轴方向，观测示意图如图5：

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 观测示意图

Fig.5 Observation diagram

天线发射电磁波被距离R处波束范围内云粒子散射，其散射电磁信号可表示为：

E_{r e c}^{(h, v)} = A^{(h, v)} (R, t) S (D) e x p {- j φ (R)} e^{j ψ (t)} e^{j ω t}

（19）

上标 $h 、 v$ 代表极化特性， R 代表位置矢量 R （x， y， z）， $S (D)$ 是粒径为D粒子的散射振幅，同时：

A^{(h, v)} (R, t) = \frac{A_{0}}{R^{2}} \sqrt[]{\frac{π G_{t} G_{r}}{k^{2}}} f {(α, φ)}^{2}

（20）

其中： $φ (R)$ 是相位传播因子； $G_{t}, G_{r}$ 分别是发射；接收天线波束视轴方向上的增益； $φ (R) = 2 k R = 2 k \sqrt[]{x^{2} + y^{2} + z^{2}}; k = \frac{2 π}{λ} 是波数$ ； $f (α, φ)$ 是天线方向图函数。

设风速方差在各方向上相同，即：

σ_{w x}^{2} = σ_{w y}^{2} = σ_{w z}^{2} = C

（21）

其中： $σ_{v_{f o b}}^{2}$ 是云粒子垂直下落速度谱的方差。假设天线方向图采用圆对称高斯形式：

{|f (θ, φ)|}^{2} = e x p \{- 4 I n 2 [{(\frac{α}{α_{1}})}^{2} + {(\frac{φ}{φ_{1}})}^{2}]\}

（22）

其中： $α_{1}$ 和 $φ_{1}$ 分别为天线3 dB波束宽度。则风切变对于高斯型天线方向图的雷达产生的谱展宽^［10］：

σ_{r}^{2} = \frac{(κ_{α}^{2} + κ_{φ}^{2}) {α_{1}}^{2} R^{2}}{16 I n 2} + {(\frac{0.34 κ_{r} c τ}{2})}^{2}

（23）

其中： $κ_{α}$ 、 $κ_{φ} 、 κ_{r}$ 是球坐标下风切变分量。 $σ_{m o v e}^{2}$ 表示有限的波束宽度内卫星运动引起的谱展宽，与天线3 dB波束宽度和卫星在速度矢量和波束视轴方向的平面内且垂直于波束方向的速度分量有关：

σ_{m o v e}^{2} = \frac{{θ_{1}}^{2} v_{p l}^{2}}{16 I n (2)} (t a n^{2} α s i n^{2} φ + 1) c o s^{2} α

（24）

各因素引起的速度谱展宽彼此独立，总的谱展宽可以表示为各个谱方差的和^［10］：

{σ_{t o t a l}}^{2} = {σ_{m o v e}}^{2} + {σ_{r}}^{2} + {σ_{v f o b}}^{2} + {σ_{w s}}^{2}

（25）

卫星运动引起的谱展宽受观察方位角的影响，在方位角由0°~90°变化的过程中， $σ_{m o v e}$ 范围由式（24）计算得到在2.79~3.70 m/s，风切变引起的谱展宽 $σ_{r}$ 依赖于风切变常量 $κ$ ，其范围通常在0.001~0.01/s，通常取 $κ = 0.005 / s$ ^［10］，若取对应的 $κ_{α}$ 、 $κ_{φ} 、 κ_{r}$ 3个分量大小相等，各分量值约为0.003/s。在轨道高度为500 km时，根据式（23）和表1中的参数，天线波束宽度为0.1°，可以计算得到不同风切变常量（0.001/s~0.01/s）引起的谱方差范围0.1~9.69 m²/s²。大气中云粒子垂直下落引起的谱宽 $σ_{v_{f o b}}$ 不会超过1 m/s，风速方差及湍流引起谱展宽 $σ_{w s}$ 在1~4 m/s^［10］，总的谱展宽如表2所示：

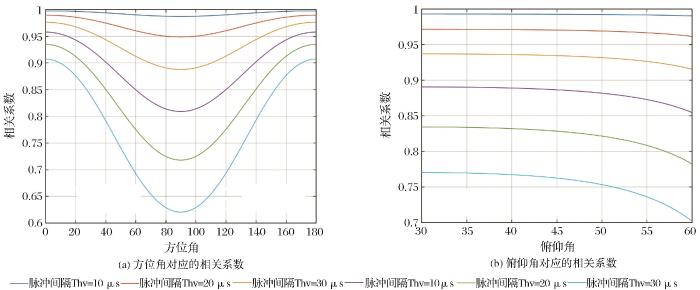
各参量的变化范围分别表示常规天气情况和极端天气情况下的数值。卫星运动引起的谱宽和观测方位角有关，而实际上风速及云粒子运动引起的谱展宽表现为速度方差在雷达波束视轴上的投影，其值也受到俯仰角的影响，谱宽的变化会影响回波信号的相关性。相关系数随观测方位角和俯仰角的变化关系如下所示，依据表2中各参数的范围，选取的仿真条件为风速标准差1 m/s，云粒子下落的多普勒速度谱标准差为0.5 m/s，卫星轨道高度为500 km，风切变分量 $κ_{α}$ = $κ_{φ} = κ_{r} =$ 0.003 /s，脉冲时宽为3.3 μs，天线波束宽度为0.1°

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同方位角和俯仰角下的相关系数

Fig.6 Correlation coefficient at different azimuth and elevation angles

可以看出脉冲间隔越大，相关系数越小，方位角为0°时（对应前视），脉冲间相关性更强，当方位角为90°时（对应于正侧视），相关系数降低，这主要由于平台运动引起的多普勒衰落在此方位向上的谱展宽最大，导致信号去相关严重。俯仰角对相关系数的影响在脉冲间隔较小时不明显，随着观测仰角的增大，相关系数降低。

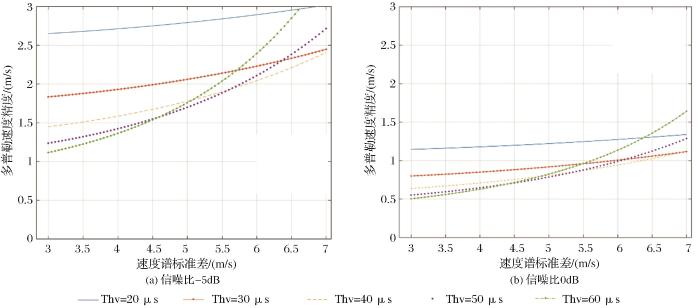
谱宽不仅在不同观测角度下影响回波信号的相关性，其大小还会直接影响速度测量精度。以下为不同谱展宽对测量速度精度的影响规律。脉冲重复频率为4 KHz。依据表1选取观测单元内多普勒速度标准差 $σ_{v}$ 变化范围为3~7 m/s，分别对应常规天气情况和极端天气条件下的谱展宽。H-V脉冲对间隔 $T_{h v}$ 分别取20 μs、30 μs、40 μs、50 μs、60 μs。脉冲对累积数为200。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 速度精度与谱宽的关系

Fig.7 Relationship between velocity accuracy and spectral width

可以看出-5 dB下速度精度均大于1 m/s。无法满足观测需求，随谱宽增加，各脉冲间隔下速度方差均增加，测速精度减小。当信噪比为0dB时随着谱宽的增加，速度测量精度均下降，在谱宽较小时（<4.5 m/s），脉冲间隔 $T_{h v}$ 越大速度测量精度越高。但当谱宽增加，如在强风切变和强对流区，脉冲对间隔的增加会引起测速精度的下降。在该信噪比下30~40 μs的H⁃V间隔在常规天气和极端天气条件下均能实现较高的测量精度。

3.3　波束宽度的影响

天线口径越大，波束宽度越窄，方位向分辨率越高，同时波束范围内多普勒衰落及风切变引起的谱展宽越小，速度精度越高，但考虑运用在卫星上的成本和难度，较大的天线难以实现。以下是天线波束宽度对速度测量精度的仿真结果，仿真条件为：风速标准差1 m/s，云粒子下落速度的多普勒速度谱宽为0.5 m/s，卫星轨道高度为500 km，观测俯仰角41°，云层高度100 m，风切变分量 $κ_{α}$ = $κ_{φ} = κ_{r} =$ 0.003 /s，脉冲时宽为3.3 μs，观测方位角为90°信噪比分别为⁃5 dB、0 dB、10 dB、15 dB。脉冲对累积数为200。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 速度精度与波束宽度的关系

Fig.8 Relationship between velocity accuracy and beam width

可以得出，速度测量精度随着波束宽度增加而降低。一方面因为宽的波束会使分辨单元内谱展宽更严重；另一方面，采用更宽的波束还会降低观测视轴方向天线增益，降低回波信噪比与灵敏度。当脉冲对间隔较小（10 μs~20 μs）时，速度精度对波束宽度的变化不敏感。60 μs的脉冲间隔下测速性能会随波束宽度增加迅速恶化。0.1°天线对应的天线尺寸约3 m，更宽的波束对应更小的天线尺寸，更易用于星上实现。结果表明，使用0.2°的波束宽度，当信噪比高于0 dB时，在脉冲间隔为30 μs~40 μs区间范围内，可以使速度精度小于1.35 m/s，这能够满足NWP对径向风数据同化需求。使用小尺寸天线对测量性能的影响还可以通过提高发射功率以增加信噪比实现精度要求。

3.4　交叉极化的影响

对于极化分集脉冲对方法，需要考虑极化串扰的影响。交叉极化信号的产生源于气象目标的去极化效应。融化层的水凝物以及柱状冰晶等可以产生高达⁃12 dB的线性去极化比（LDR），根据NRC机载W波段雷达的测量，地表和海洋表面也会产生强烈的去极化，其值分别在⁃10 dB和⁃15 dB左右^［6］。交叉极化引入的估计误差和云的反射率结构剖面、LDR剖面以及v⁃h脉冲对的间隔有关。串扰信号来自不同的距离门，因此独立于同极化信号，并不会引起速度估计的偏差，但作为随机误差会增加速度估计方差。

根据Pazman等^［11］的研究，在脉冲对样本数量为 $M$ 时，速度估计误差为：

v a r_{v h} ({\hat{v}}_{d} (r)) = \frac{1}{π^{2}} {(\frac{λ}{4 T_{v h}})}^{2} \frac{v a r (|R_{v h} (r, T_{v h})|)}{2 {|R_{v h} (r, T_{v h})|}^{2}} = \frac{V_{m a x}^{2}}{2 M {[π |R_{v h} (r, T_{v h})|]}^{2}} [P_{c o}^{2} (r) - {|R_{v h} (r, T_{v h})|}^{2} + P_{c o} (r) P_{c r o s s} (r + Δ r) + 2 P_{c o} (r) P_{n} + P_{c r o s s} (r - Δ r) P_{c o} (r) + P_{c r o s s} (r - Δ r) P_{c r o s s} (r + Δ r) + P_{c r o s s} (r - Δ r) P_{n} + P_{n} P_{c r o s s} (r + Δ r) + P_{n}^{2}]

（26）

其中：

P_{c o} (r) = 〈{|V_{v v} (r)|}^{2}〉 = 〈{|V_{h h} (r)|}^{2}〉

P_{c r o s s} (r) = 〈{|V_{v h} (r)|}^{2}〉 = 〈{|V_{h v} (r)|}^{2}〉

P_{n} = 〈{|N_{v}|}^{2}〉 = 〈{|N_{h}|}^{2}〉

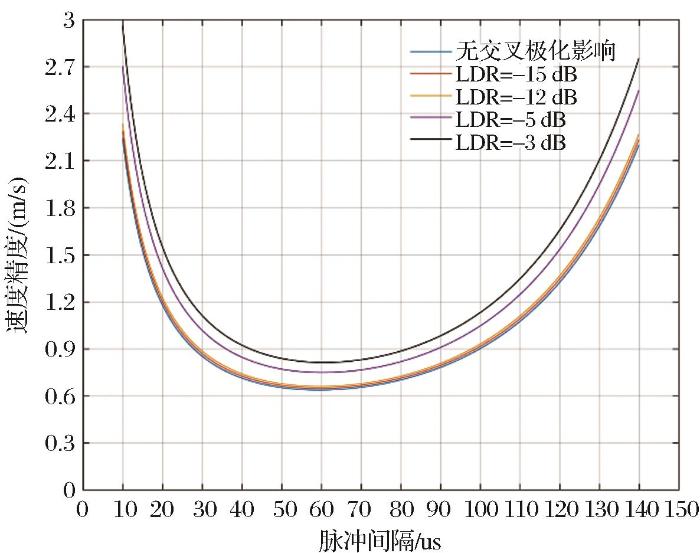
以下比较了不同LDR和无交叉极化串扰影响时速度精度的结果。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 受LDR影响的速度精度和脉冲间隔的关系

Fig.9 Relationship between velocity accuracy and pulse pair interval affected by LDR

随着交叉极化影响的增强（LDR增加），速度测量精度降低，而且在脉冲间隔较小时，受交叉极化影响更加显著。具体表现为，20 μs的脉冲间隔下，LDR为-3 dB时速度估计精度约为1.6 m/s，此时无极化串扰下的速度精度约在1.2 m/s；当脉冲间隔为60 μs时，-3 dB的LDR下速度精度约为0.8 m/s，而无极化串扰下的估计精度约0.6 m/s。

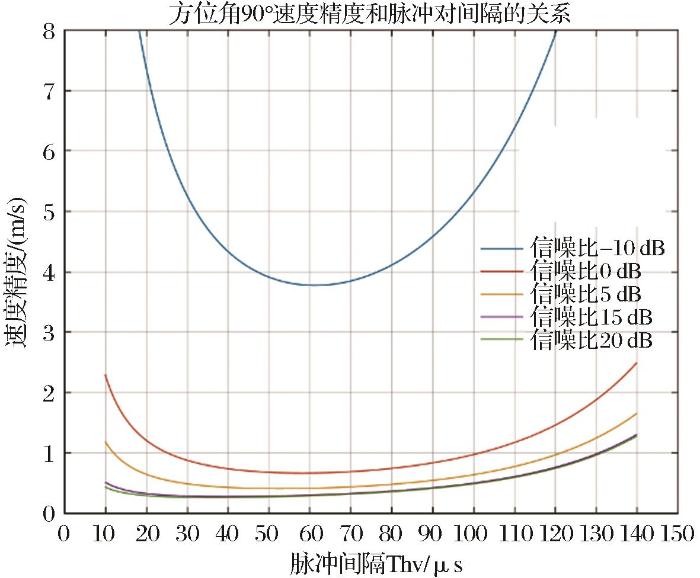
3.5　脉冲间隔的影响

不同 $T_{h v}$ 脉冲间隔下信号的相关性不同，如下是速度测量精度在方位角上90°时的仿真结果。仿真条件为：风速标准差为１ m/s，云粒子下落的多普勒速度谱标准差为0.5 m/s，LDR为-15 dB，卫星轨道高度为500 km，风切变分量 $κ_{α}$ = $κ_{φ} = κ_{r} = 0.003 / s$ ，脉冲时宽为3.3 μs，天线波束宽度为0.1°。脉冲重复频率4 kHz，脉冲对累积数为200。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 速度精度和脉冲间隔的关系

Fig.10 The relationship between speed accuracy and pulse interval

结果表明，速度精度与脉冲间隔有关，随着脉冲间隔的增加，速度精度呈现出现增大后减小，原因在于当脉冲对间隔较小时，回波信号多普勒相位分辨受到影响，即由于较短的脉冲间隔导致多普勒频移在该间隔内使相位的改变不明显；脉冲间隔增大，会使信号的相关性减小，降低了测速精度。SNR也会影响速度精度，在-10 dB信噪比下，速度误差大于3 m/s，无法满足测量需求。

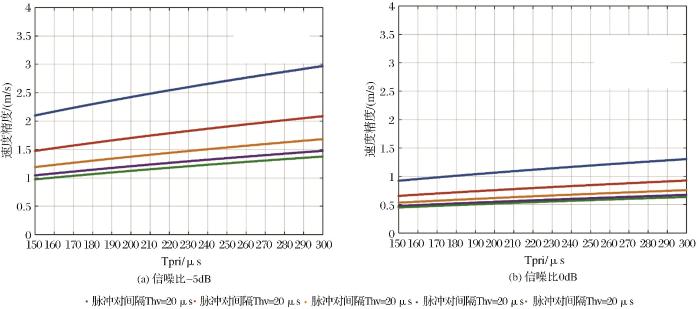
3.6　脉冲对重复周期的影响

以下讨论了不同脉冲对重复周期（PRT）对速度估计精度的影响规律。仿真条件为：风速标准差1 m/s，云粒子下落速度的多普勒速度谱标准差为0.5 m/s，LDR为-15 dB，卫星轨道高度为500 km，风切变分量为0.003/s，脉冲宽度为3.3 μs，天线波束宽度为0.1°，观测方位角为90°，俯仰角41°，其中信噪比分别为-5 dB和0 dB。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 速度精度与PRT的关系

Fig.11 Relationship between velocity measurement accuracy and PRT

可以看出PDPP方法的速度估计精度随脉冲对重复周期的增加而降低，一方面式（14）中包含参数 $T_{p r i}$ 本身的影响，另一方面，在相同的路径积分长度上，脉冲对重复周期的增加会导致累积样本数减少，从而降低速度估计精度。相对于信噪比， $T_{p r i}$ 在低信噪比下对结果影响显著。信噪比增大，测量精度对 $T_{p r i}$ 的敏感性降低，信噪比影响占主导地位。

4 讨论

云内风场的探测基于云粒子后向散射的雷达回波，根据极化分集脉冲对算法，仿真分析了影响径向速度测量能力的因素。文中主要考虑雷达系统参数和气象目标谱展宽特征对速度测量精度的影响。实测中，引起测量精度的误差来源还有天线指向误差、非均匀波束填充效应及云粒子内部多次散射效应，这些误差的影响并未详细提及，相应的校正方法可见相关文献。

本文的仿真模型建立在对云粒子的非相干散射回波进行脉冲对处理，但对于实测的气象条件，由于湍流脉动常伴随时间或空间上的相关性，实测中散射还会有大气粒子的相干散射，在94 GHz的探测频段上，该散射较弱，通常仅考虑云粒子的非相干散射效应，但建立精确的散射回波模型有助于能得到更严谨的结果。

5 结语

本文分析了W波段星载多普勒雷达云内大气风场速度测量能力，根据回波信号的相关函数结合极化分集脉冲对算法仿真了方位角、脉冲间隔、信噪比、脉冲对重复周期以及天线波束宽度对PDPP方法速度估计精度的影响规律。结果表明，脉冲重复频率设计需满足探测范围的要求，考虑云的分布范围及PDPP时序特点，PRF不能超过5KHz，但PRF太低将导致观测样本数的减小，降低脉冲累积数，其范围可在3.5~5 KHz之间。天线波束宽度的影响体现在相同天气条件下，更宽的波束会使相关函数中谱展宽更大，从而影响测量精度；同时更宽的天线波束也会导致增益的降低，信噪比减小。速度谱宽对精度的影响体现在谱宽较小时较大的脉冲对间隔精度更高，但极端天气条件下，谱宽变大，更大的脉冲对间隔的速度测量能力会下降。综合各种因素考虑，脉冲间隔的范围在30~50 μs，波束宽度0.1°的条件下能对反射率因子-20 dBZ的云速进行测量，并能适应绝大多数天气条件；而使用0.2°波束宽度的天线则脉冲间隔选取30~40 μs之间，能达到探测灵敏度约-12 dBZ。本文的仿真结果对星载毫米波雷达采用PDPP方法进行云内大气风场多普勒测量的系统参数设计具有指导意义。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ILLINGWORTH

A J

， BATTAGLIA

， BRADFORD

， et al.

Wivern：A new satellite concept to provide global in-cloud winds，precipitation， and cloud properties

［J］.Bulletin of the American Meteorological Society，2018，99（8）：1669-1687.

[本文引用: 2]

[2]

BAKER

E W

Lidar-measured wind profiles： The missing link in the global observing systems

［J］ Bulletin of the American Meteorological Society，2014，95（4）：543–564.

[本文引用: 1]

[3]

MCNALLY

A P

A note on the occurrence of cloud in meteorologically sensitive areas and the implications for advanced infrared sounders

［J］. Quarterly Journal of the Royal Meteorological Society， 2002， 128（585）： 2551-2556.

[本文引用: 1]

[4]

BATTAGLIA

， DHILLON

， ILLINGWORTH

Doppler W-band polarization diversity spaceborne radar simulator for wind studies

［J］. Atmospheric Measurement Techniques， 2018， 11（11）： 5965-5979.

[本文引用: 1]

[5]

DOVIAK

R J

， SIRMANS

Doppler Radar with Polarization Diversity

［J］. Journal of Atmospheric Sciences 1973， 30（4）： 737-738

[本文引用: 1]

[6]

BATTAFLIA

， WOLDE

， ILLINGWORTH

， et al.

Implementation of polarization diversity pulse-pair technique using airborne W-band radar

［J］. Atmospheric Measurement Techniques， 2019， 12（1）： 253-269.

[本文引用: 2]

[7]

ZHANG

Peichang

. Radar Meteorology［M］. Beijing： Meteorological Press， 1988.

[本文引用: 1]

张培昌

. 雷达气象学［M］. 北京：气象出版社， 1988.

[本文引用: 1]

[8]

KOBAYASHI

， KUMAGAI

， KUROIWA

A proposal of pulse-pair doppler operation on a Spaceborne Cloud-Profiling Radar in the W band

［J］. Journal of Atmospheric and Oceanic Technology，2002，19（9）：1294-1306.

[本文引用: 1]

[9]

ZRINC.

Spectral moment estimates from correlated pulse pairs

［J］. IEEE Transactions on Aerospace and Electronic Systems， 1977， AES-13（4）： 344-354.

[本文引用: 1]

[10]

AMAYENC， PAUL， TESTUD， et al.

Proposal for a Spaceborne Dual-Beam Rain Radar with doppler capability

［J］. Journal of Atmospheric and Oceanic Technology，1993，10（3）： 262-276

[本文引用: 4]

[11]

PAZMANY

A L

， GALLOWAY

J C

， MEAD

J B

， et al.

Polarization diversity pulse-pair technique for Millimetre-Wave Doppler Radar measurements of severe storm features

［J］. Journal of Atmospheric and Oceanic Technology， 1998， 16（12）： 1900-1911.

[本文引用: 1]

Wivern：A new satellite concept to provide global in-cloud winds，precipitation， and cloud properties

2018

... 大气风场是重要的气象要素，将三维风场的测量结果同化到天气预报模式中，改进数值天气预报（NWP）的初始条件，将显著提高预报精度.世界气象组织明确指出，全球风廓线“对于所有尺度和所有纬度的业务天气预报至关重要”^［1］.全球风场的精确测量也能帮助推动一些关键气候变化问题的研究.有研究表明，大气环流在10 a时间尺度上的改变，其中一些变化可能是受到温室气体的作用影响，而研究所依赖的气候模型和数据集并不能对大尺度环流的变化提供完整信息.由于热带大气的大部分地区没有实测的风廓线，考虑到风场在质量—运动平衡关系中的主导地位，风廓线测量对于热带气旋、季风环流和非洲东风急流等热带现象，其预测水平将会有很大的提升^［2］.高分辨率的全球大气风场数据是WMO迫切需要的，然而获取全球风场也面临许多挑战. ...

... 地基风廓线雷达是获取风场信息的重要手段，多雷达组网观测技术已经成熟，但该方法受到地形地貌限制，在海洋及偏远山地无法布设观测站，使得这些区域观测数据匮乏.星载微波散射计通过测量海面后向散射系数反演海表面风场，但不能用于陆地风场，且无法获得海洋上空的大气风场.云导风技术通过静止轨道气象卫星成像获得连续时序的卫星云图，捕捉云图上示踪云团的运动轨迹推算风速和风向，缺点在于无法获得云内部垂直尺度的对流特征.低轨卫星上使用大气目标（气溶胶，云雨粒子）作为风的“示踪物”的多普勒主动传感器（激光雷达和雷达）来进行全球风测量被认为是一种有效手段.2018年发射的欧空局风神任务提供了第一个多普勒激光雷达测量晴空和薄冰云中的视线风.McNally^［3］的研究表明，多云区域的风观测能提升预报潜力.星载多普勒激光测风雷达适用于晴空大气风场测量，但在面对云雨条件时，由于激光无法穿透云层，因而不能获取云内风的信息.ESA-JAXA EarthCARE任务通过天底点指向的W波段多普勒云雷达提供云粒子的垂直速度，首次实现从太空观测冰晶沉积速率、上升对流和下沉气流的能力，但该多普勒雷达无法在深云系统中提供水平风场^［4］.水平风的测量需要偏离天底点且具有多波束的立体雷达或具有扫描能力的多普勒雷达，通过对同一观测单元实现不同方位角的观测得到的径向速度估计来反演水平风分量.多普勒速度精度要求取决于应用，NWP对低对流层水平风的实现目标是误差小于2 ms^-1，水平分辨率15 km，垂直分辨率0.5 km^［1］. ...

Lidar-measured wind profiles： The missing link in the global observing systems

2014

A note on the occurrence of cloud in meteorologically sensitive areas and the implications for advanced infrared sounders

2002

Doppler W-band polarization diversity spaceborne radar simulator for wind studies

2018

Doppler Radar with Polarization Diversity

1973

... 实现星载云雷达多普勒径向速度的测量是反演三维风场的基础，云雨粒子对W波段频率的电磁波表现出明显的散射特性，而多普勒雷达通过测量随风运动的水凝物粒子的后向散射信号的多普勒频移，根据多普勒频移和径向速度的关系实现速度探测.多普勒频率的估计方法有基于DFT的谱分析方法，通过频谱的一阶矩和二阶矩得到平均频率和谱宽的估计，该方法需要在高采样率下进行频谱变换，运算较为复杂.星载多普勒雷达对多普勒频率的估计多采用时域的脉冲对算法（Pulse Pair Processing， PPP），通过发射脉冲对形式的信号，若探测目标存在径向运动，则接收到的一对脉冲信号会因多普勒频移在脉冲对间隔内的积累表现出相位差，利用相位差估计平均频移从而得到速度的估计，它可以直接在时域完成速度估计，处理上更为方便.其中，脉冲对间隔受最大无模糊距离和最大无模糊速度的约束.星载平台上的脉冲对操作相比地基或机载平台会面临更多的困难，因为卫星的高速运动引起的多普勒衰落使信号的去相关严重，而为了满足足够的探测范围（最大无模糊距离），对于0~20 km高度范围分布的云，接收窗长度至少为133.3 us，对应W波段电磁波测量的最大无模糊速度为6 m/s.在极端天气情况下，如台风飑线过境时常伴随短时间风向突变、风速增大情况，速度可能超过40 m/s，在这样的脉冲间隔下会产生速度模糊.为了增强风暴、强对流等气象条件下速度测量范围，Doviak等^［5］提出了极化分集脉冲对（Polarization Diversity Pulse-Pair，PDPP）算法，通过发射时间间隔更短的正交极化脉冲，用两个通道同时接收两个正交极化脉冲的后向散射信号，进一步减小脉冲间隔来提高最大无模糊速度.但PDPP方法也会存在交叉极化串扰效应等影响，其速度测量精度需结合脉冲对算法估计性能加以分析. ...

Implementation of polarization diversity pulse-pair technique using airborne W-band radar

2019

... H和V通道中接收的复电压信号分别为

V_{H}

和

V_{V}

， v-h脉冲对和h-v脉冲对的相关函数分别记为

R_{v h}

，

R_{h v}

，则M个样本累积后的相关函数为^［6］：τ ...

... 对于极化分集脉冲对方法，需要考虑极化串扰的影响.交叉极化信号的产生源于气象目标的去极化效应.融化层的水凝物以及柱状冰晶等可以产生高达⁃12 dB的线性去极化比（LDR），根据NRC机载W波段雷达的测量，地表和海洋表面也会产生强烈的去极化，其值分别在⁃10 dB和⁃15 dB左右^［6］.交叉极化引入的估计误差和云的反射率结构剖面、LDR剖面以及v⁃h脉冲对的间隔有关.串扰信号来自不同的距离门，因此独立于同极化信号，并不会引起速度估计的偏差，但作为随机误差会增加速度估计方差. ...

1988

... 信噪比会影响速度估计精度.天线接收波束采样体积内云粒子的后向散射信号，接收机输出的平均功率和云粒子对电磁波的散射特性有关.气象雷达方程描述了云的反射率因子强度和回波功率的关系.

P_{t}

为雷达的发射功率，G是观测视轴上天线增益（收发同天线），L为系统损耗，k是衰减系数，

α 、 φ

分别为俯仰和方位向波束宽度，

|K|

与水的介电常数有关.c表示电磁波传输速度，τ是发射脉冲宽度；λ是雷达发射的电磁波波长；Z代表气象目标反射率因子，对距离

r

处的云目标，接收到的回波功率

P_{r}

为^［7］： ...

1988

P_{t}

为雷达的发射功率，G是观测视轴上天线增益（收发同天线），L为系统损耗，k是衰减系数，

α 、 φ

分别为俯仰和方位向波束宽度，

|K|

与水的介电常数有关.c表示电磁波传输速度，τ是发射脉冲宽度；λ是雷达发射的电磁波波长；Z代表气象目标反射率因子，对距离

r

处的云目标，接收到的回波功率

P_{r}

为^［7］： ...

A proposal of pulse-pair doppler operation on a Spaceborne Cloud-Profiling Radar in the W band

2002

... 雷达波束照射的体积单元内，假设各云粒子运动是随机的且相互独立，回波信号为每个粒子散射结果的非相干叠加.由中心极限定理，大量独立的随机变量之和满足高斯分布，即多普勒速度谱满足高斯分布，根据多普勒速度和多普勒频率的线性关系，其回波的功率谱具有如下形式^［8］： ...

Spectral moment estimates from correlated pulse pairs

1977

...

δ (τ)

是冲击函数，对于H极化和V极化脉冲对间隔

T_{h v}

，脉冲重复间隔

T_{p r i}

的极化分集脉冲对（PDPP）时序，不考虑交叉极化影响时，极化分集脉冲对算法的多普勒速度测量方差^［9］表示为： ...

Proposal for a Spaceborne Dual-Beam Rain Radar with doppler capability

1993

... 其中：

α_{1}

和

φ_{1}

分别为天线3 dB波束宽度.则风切变对于高斯型天线方向图的雷达产生的谱展宽^［10］： ...

... 各因素引起的速度谱展宽彼此独立，总的谱展宽可以表示为各个谱方差的和^［10］： ...

... 卫星运动引起的谱展宽受观察方位角的影响，在方位角由0°~90°变化的过程中，

σ_{m o v e}

范围由式（24）计算得到在2.79~3.70 m/s，风切变引起的谱展宽

σ_{r}

依赖于风切变常量

κ

，其范围通常在0.001~0.01/s，通常取

κ = 0.005 / s

^［10］，若取对应的

κ_{α}

、

κ_{φ} 、 κ_{r}

3个分量大小相等，各分量值约为0.003/s.在轨道高度为500 km时，根据式（23）和表1中的参数，天线波束宽度为0.1°，可以计算得到不同风切变常量（0.001/s~0.01/s）引起的谱方差范围0.1~9.69 m²/s².大气中云粒子垂直下落引起的谱宽

σ_{v_{f o b}}

不会超过1 m/s，风速方差及湍流引起谱展宽

σ_{w s}

在1~4 m/s^［10］，总的谱展宽如表2所示： ...

... ［10］，总的谱展宽如表2所示： ...

Polarization diversity pulse-pair technique for Millimetre-Wave Doppler Radar measurements of severe storm features

1998

... 根据Pazman等^［11］的研究，在脉冲对样本数量为

M

时，速度估计误差为： ...

〈

〉