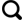西宁市北山地区林家崖滑坡发育特征及稳定性分析
1
2015
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
西宁市北山地区林家崖滑坡发育特征及稳定性分析
1
2015
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
顾及多动态环境因子的滑坡演化规律研究——以西宁市9大滑坡区为例
1
2023
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
顾及多动态环境因子的滑坡演化规律研究——以西宁市9大滑坡区为例
1
2023
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
重大地质灾害隐患早期识别中综合遥感应用的思考与建议
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
重大地质灾害隐患早期识别中综合遥感应用的思考与建议
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
卫星雷达遥感在滑坡灾害探测和监测中的应用:挑战与对策
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
卫星雷达遥感在滑坡灾害探测和监测中的应用:挑战与对策
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
运用水准和InSAR的地面沉降监测数据融合方法
1
2015
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
运用水准和InSAR的地面沉降监测数据融合方法
1
2015
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
时序InSAR水库大坝形变监测应用研究
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
时序InSAR水库大坝形变监测应用研究
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR变形监测方法与研究进展
1
2017
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR变形监测方法与研究进展
1
2017
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
利用附加系统参数的GPS-InSAR综合形变模型建立三维形变场
1
2017
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
利用附加系统参数的GPS-InSAR综合形变模型建立三维形变场
1
2017
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR矿区地表三维形变监测与预计研究进展
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR矿区地表三维形变监测与预计研究进展
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
WANG Zhiwei,Research on resolving of three-dimensional displacement from multi-source InSAR data
1
2019
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
Integrated satellite interferometry in southern california
1
1997
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
The Double Interpolation and Double Prediction(DIDP) Approach for InSAR and GPS Integration
1
2000
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
GPS-DInSAR集成监测的改进定权方法与仿真实验分析
1
2012
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
GPS-DInSAR集成监测的改进定权方法与仿真实验分析
1
2012
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
Three-dimensional surface displacements from InSAR and GPS measurements with variance component estimation
1
2012
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
融合InSAR和GNSS的三维形变监测:利用方差分量估计的改进SISTEM方法
1
2021
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
融合InSAR和GNSS的三维形变监测:利用方差分量估计的改进SISTEM方法
1
2021
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR与GPS数据融合在变形监测中的应用研究
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
InSAR与GPS数据融合在变形监测中的应用研究
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
融合单视线D-InSAR和BK模型的煤矿地表三维变形动态监测方法研究
1
2023
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
融合单视线D-InSAR和BK模型的煤矿地表三维变形动态监测方法研究
1
2023
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
基于GPS-InSAR数据融合的地表三维形变模型建立方法研究
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
基于GPS-InSAR数据融合的地表三维形变模型建立方法研究
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
GPS与InSAR技术在滑坡监测中的应用研究
1
2006
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
GPS与InSAR技术在滑坡监测中的应用研究
1
2006
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
3D displacement field of wenchuan earthquake based on iterative least squares for virtual observation and GPS/InSAR Observations
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
基于时序InSAR和GPS技术的北京平原区地表三维形变场特征
1
2022
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
基于时序InSAR和GPS技术的北京平原区地表三维形变场特征
1
2022
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
Modeling the posteruptive deformation at okmok based on the GPS and InSAR time series: Changes in the shallow magma storage system
1
2020
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
An InSAR atmospheric correction method based on GNSS and machine learning
1
2023
... 随着城市基础设施建设规模的逐步扩大,地质灾害频发.常见的诸如泥石流、滑坡、地面沉陷等地质灾害多因为地表形变引起的[1-2],由此对地表三维形变监测[3]具有重大现实意义.目前,地表形变监测方法主要有全球导航卫星定位系统 (GNSS) 和卫星雷达干涉测量[4](InSAR)两种.其中,GNSS 技术的优势在于具有多方向、高精度、自动化观测等特点,但受限于监测设备,其GNSS点位稀疏,一些灾害点人工无法布设控制点[5].InSAR技术的优势在于其具有大范围、高精度、不需要地面架设设备等特点[6].人工无法布设控制点的地方,InSAR都可以覆盖到.但InSAR受SAR卫星观测周期的影响[7],同一个位置监测周期长,且只能获取该位置视线向(LOS)上的一维形变,制约了InSAR监测精度[8].如何利用两者不同优点进行融合,解决高时空分辨率、高精度的三维形变场问题成为地表形变监测领域研究的热点[9-10].Bock等[11]率先提出GNSS和InSAR的融合思想,Ge等[12]提出双插双估计(DIDP)方法,该方法利用GNSS数据来提高InSAR观测值的精度,再利用InSAR反过来加密GNSS观测结果.罗海滨等[13]提出了直接分解法,该方法成功利用GNSS和InSAR的优点,算法简单,但是十分依赖GNSS的精度和GNSS插值的精度,若GNSS精度或GNSS插值精度较差,最后得到的结果会受到影响.胡俊等[14]提出了赫尔默特方差估计法,该方法根据GNSS和InSAR观测值方差的估计值反复定权,以达到两者观测值的权合理,其结果较最小二乘法有提高.汪友军等[15]利用应力应变模型结合方差分量估计算法,得到更高精度的三维地表形变结果.赵增鹏等[16]分析了对流层对InSAR的影响,通过GNSS数据处理InSAR数据中存在的对流层延迟误差,提高了D-InSAR的监测精度.江克贵等[17]提出了利用BK模型结合单视线D-InSAR的监测方法,但由于观测区域较远,可能导致了预计效果不佳.吕佳凝等[18]在直接分解法中进一步提出拟合推估法[19].该方法同样利用了GNSS数据的特性,对InSAR影像中存在的系统误差进行校正,提高了融合精度.但是方法末尾结合了最小二乘法,当有较大粗差出现时,将不能得到较好的结果.熊陆云等[20]提出了一种基于贝叶斯定理的最大后验估计准则的虚拟观测迭代最小二乘( VOILS )方法来校正GPS位移内插过程引起的误差.其对垂直方向的改善尤为明显.雷坤超等[21]利用GNSS水平精度高和InSAR垂直精度高的原理,将GNSS水平位移测量与InSAR垂直观测结合,得到了北京平原区的地表三维形变场.但是,该方法降低了GNSS的时间分辨率和InSAR的空间分辨率.薛学明等[22]基于无迹卡尔曼滤波,结合GNSS和InSAR时间序列观测模拟了火山变形,GNSS和InSAR数据拟合结果在2~4 km深度处拟合的较好.武帅莹等[23]基于机器学习的GNSS大气建模方法对InSAR进行大气改正,提升InSAR监测精度. ...
基线误差、相位误差和大气延迟误差对InSAR数据处理的影响分析
1
2010
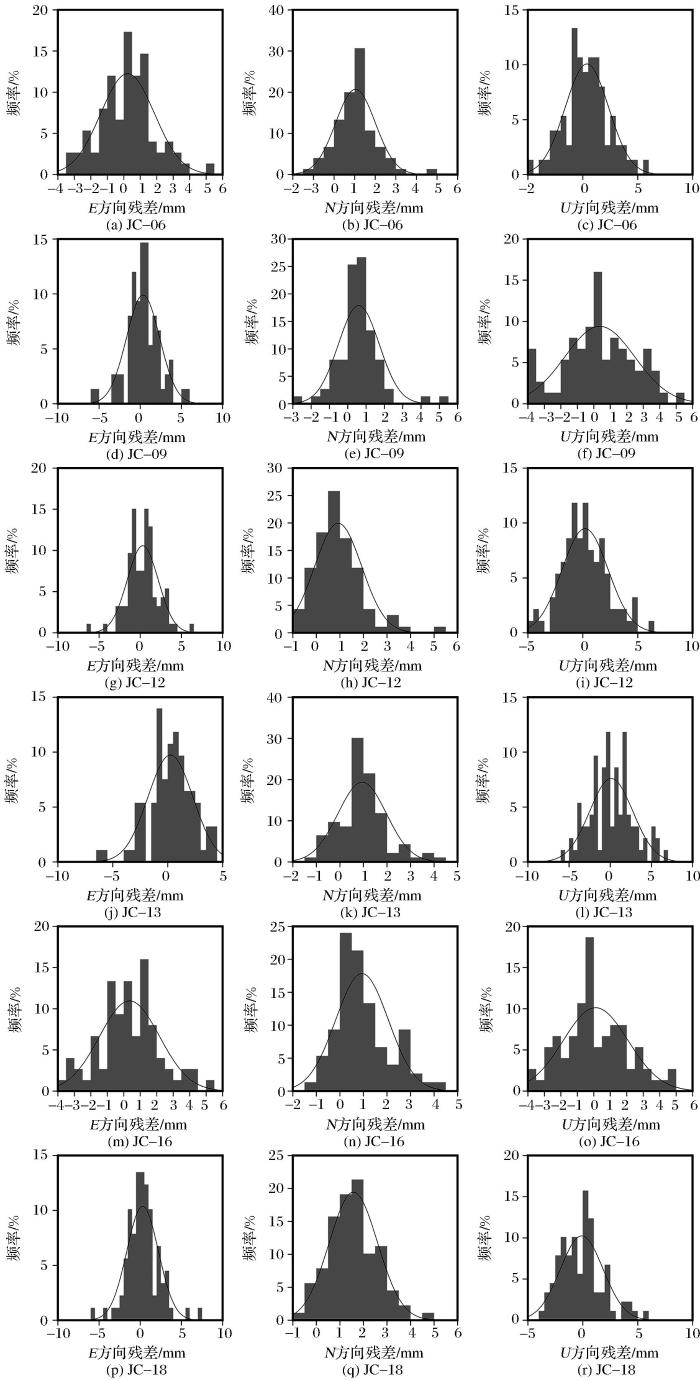
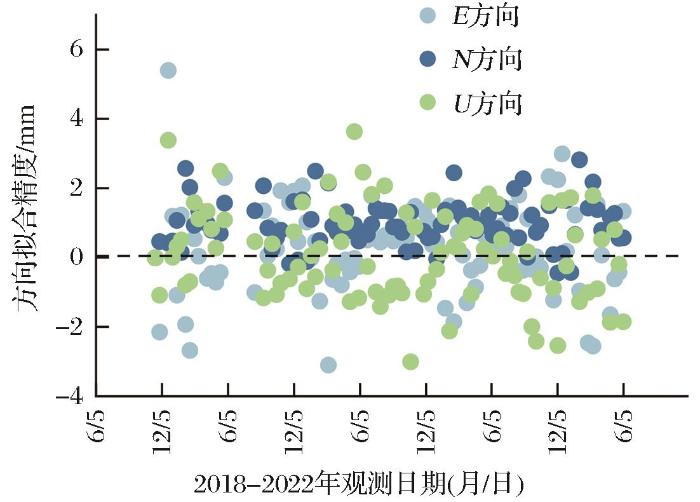
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
基线误差、相位误差和大气延迟误差对InSAR数据处理的影响分析
1
2010
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
利用GPS位移数据校正2011日本Tohoku地震的InSAR形变场
1
2017
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
利用GPS位移数据校正2011日本Tohoku地震的InSAR形变场
1
2017
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
The influence of equatorial scintillation on L-Band SAR image quality and phase
1
2016
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
Permanent scatterers in SAR interferometry
1
2001
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
GPS、InSAR数据联合解算地表三维形变场
1
2017
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
GPS、InSAR数据联合解算地表三维形变场
1
2017
... 拟合推估法是一种推估方法.该方法是通过一定的拟合法则,对数据进行推估.由于SAR卫星存在雷达参数、相位观测量和地形数据等不确定性,其误差会传播到形变结果中去[24].若直接与GNSS数据融合,其结果也包含这些误差.但是,InSAR的系统误差与GNSS存在较高的空间相关性[25],可通过GNSS数据进行削弱[26-27].将高精度的GNSS观测值对InSAR观测值进行约束,得到同点位上GNSS和InSAR观测值的差值,通过拟合法则将差值拟合出来,将差值进行校正,最后得到精度较高的InSAR观测值[28]. ...
基于BFGS法融合InSAR和GPS技术监测地表三维形变
1
2013
... 其中:为观测量;为状态矢量;为观测噪声.其中为监测点的形变量,为监测点的变形速率,3个状态向量通过最小二乘法求得[29].为观测方程设计矩阵,为一个3×3的单位阵. ...
基于BFGS法融合InSAR和GPS技术监测地表三维形变
1
2013
... 其中:为观测量;为状态矢量;为观测噪声.其中为监测点的形变量,为监测点的变形速率,3个状态向量通过最小二乘法求得[29].为观测方程设计矩阵,为一个3×3的单位阵. ...
1
2011
... 在状态方程和观测方程建好后,需给定系统初始状态.取初始时刻的形变量及方差为0,初始时刻的及对应的方差矩阵为GNSS和InSAR数据平差后的形变速率和方差.观测噪声的方差阵[30]. ...
1
2011
... 在状态方程和观测方程建好后,需给定系统初始状态.取初始时刻的形变量及方差为0,初始时刻的及对应的方差矩阵为GNSS和InSAR数据平差后的形变速率和方差.观测噪声的方差阵[30]. ...
西宁市黄土滑坡发育特征及稳定性分析
1
2013
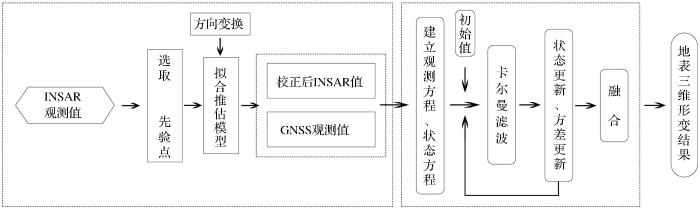
... 西宁位于中国西北,四面环山,东西呈条带状.湟水两岸(分别为南山和北山)沟壑纵横,地形切割强烈,人类工程活动强烈,生态地质环境脆弱,崩塌、滑坡、泥石流等突发性地质灾害发育,特别是滑坡、崩塌高发,对坡脚居民的生命财产构成严重威胁[31-32].研究区和GNSS站点分布如图2所示. ...
西宁市黄土滑坡发育特征及稳定性分析
1
2013
... 西宁位于中国西北,四面环山,东西呈条带状.湟水两岸(分别为南山和北山)沟壑纵横,地形切割强烈,人类工程活动强烈,生态地质环境脆弱,崩塌、滑坡、泥石流等突发性地质灾害发育,特别是滑坡、崩塌高发,对坡脚居民的生命财产构成严重威胁[31-32].研究区和GNSS站点分布如图2所示. ...
基于SBAS-InSAR技术的西宁地表形变监测
1
2021
... 西宁位于中国西北,四面环山,东西呈条带状.湟水两岸(分别为南山和北山)沟壑纵横,地形切割强烈,人类工程活动强烈,生态地质环境脆弱,崩塌、滑坡、泥石流等突发性地质灾害发育,特别是滑坡、崩塌高发,对坡脚居民的生命财产构成严重威胁[31-32].研究区和GNSS站点分布如图2所示. ...
基于SBAS-InSAR技术的西宁地表形变监测
1
2021
... 西宁位于中国西北,四面环山,东西呈条带状.湟水两岸(分别为南山和北山)沟壑纵横,地形切割强烈,人类工程活动强烈,生态地质环境脆弱,崩塌、滑坡、泥石流等突发性地质灾害发育,特别是滑坡、崩塌高发,对坡脚居民的生命财产构成严重威胁[31-32].研究区和GNSS站点分布如图2所示. ...
干涉基线对地震形变场的影响——以玛尼地震同震-震后形变场为例
1
2012
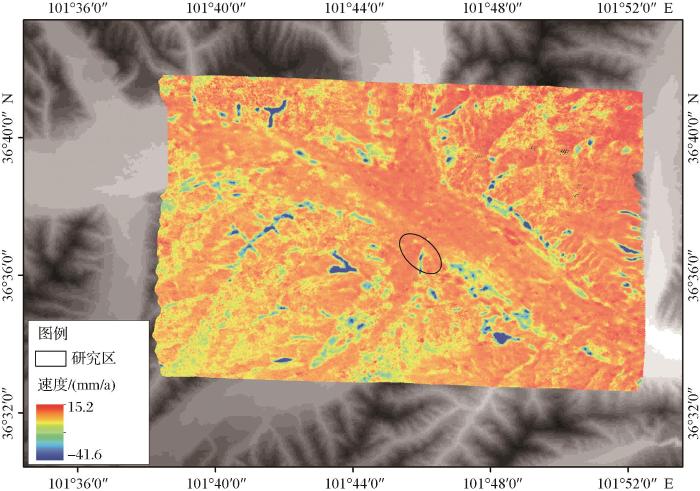
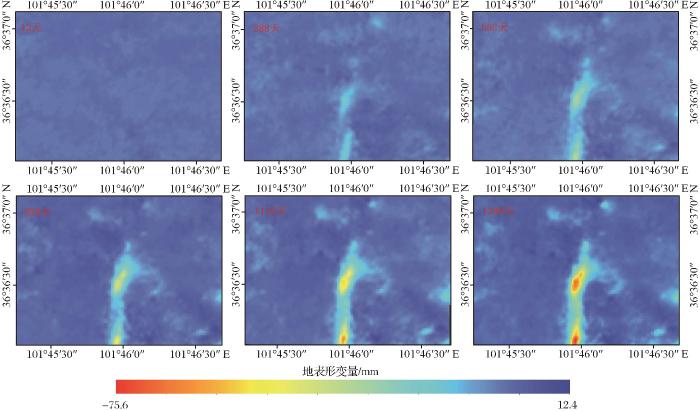
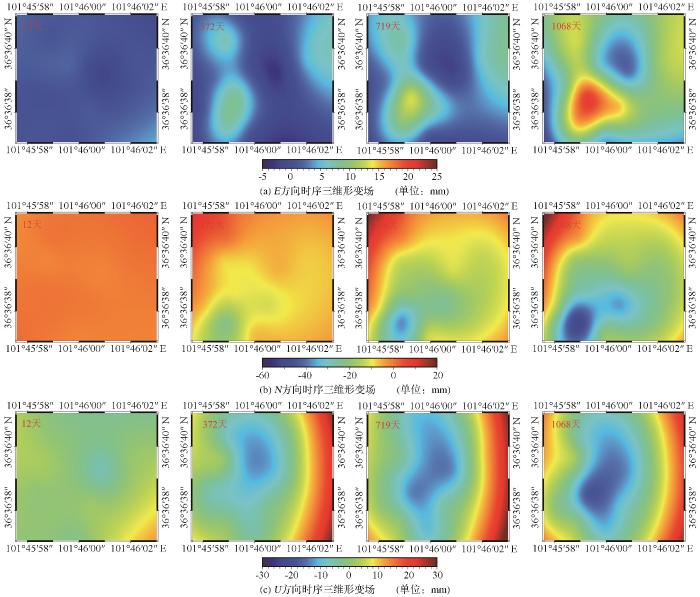
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
干涉基线对地震形变场的影响——以玛尼地震同震-震后形变场为例
1
2012
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
InSAR相位解缠算法比较及误差分析
1
2004
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
InSAR相位解缠算法比较及误差分析
1
2004
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
A refined strategy for removing composite errors of SAR interferogram
1
2013
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
SBAS技术在地面沉降监测中的应用——以武汉市为例
1
2018
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
SBAS技术在地面沉降监测中的应用——以武汉市为例
1
2018
... 研究使用ENVI SARScape软件,利用短基线集技术(Small Baseline Subset,SBAS)对所得103景Sentinel-1A卫星降轨数据和对应精轨数据进行处理.①设置时间基线、空间基线[33]阈值等相关参数.②对像对进行干涉处理并利用DRTMV4作为外部DEM数据去除干涉对地形效应.③估算和去除残余的恒定相位和解缠[34]后还存在的相位坡道[35].④若解缠结果不理想,会对干涉图做二次解缠来优化.其中,线性模型最为稳定.⑤大气延迟是InSAR中主要误差源.利用定制的高通滤波和低通滤波去除大气相位.⑥将所得SBAS结果进行编码并对位移速率图进行分析.图3为基于SBAS-InSAR技术的LOS方向2018年11月15日至2022年6月3日间地表平均形变速率图[36],黑色椭圆区域为GNSS布置区.图4为同期的地表位移时间序列图. ...
多时相Sentinel-1A InSAR的连盐高铁沉降监测分析
1
2021
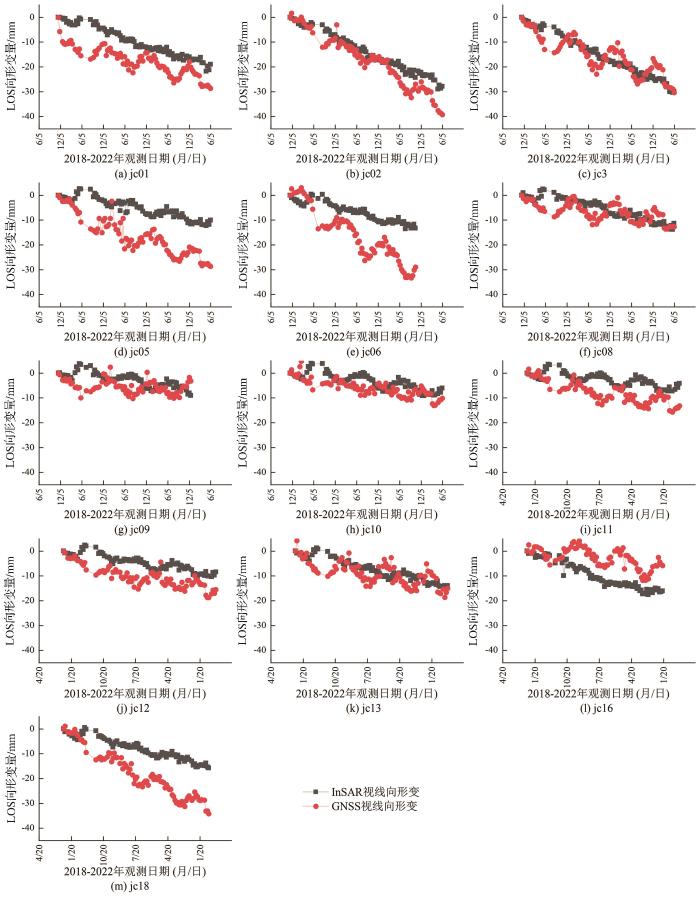
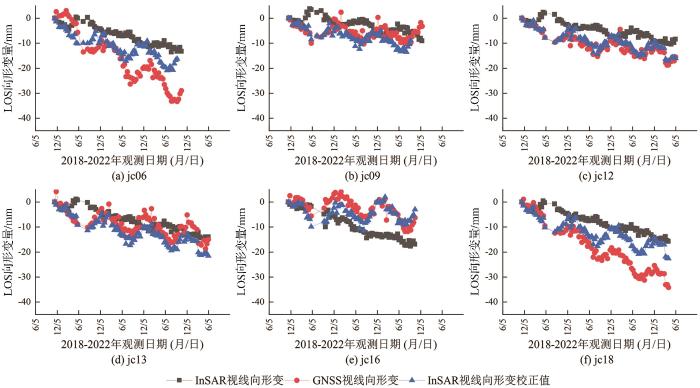
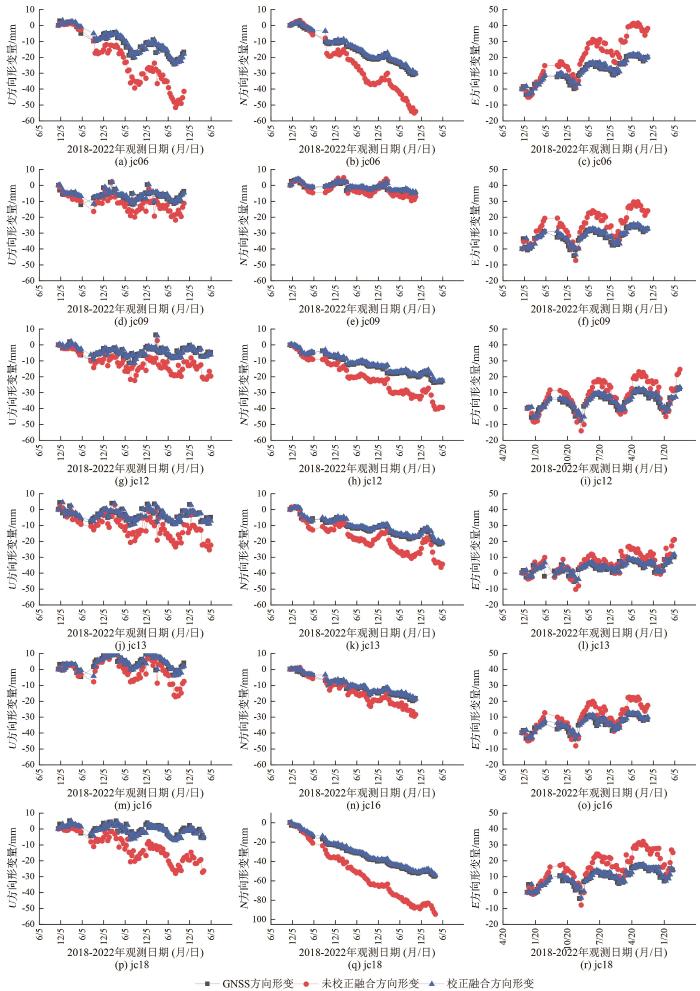
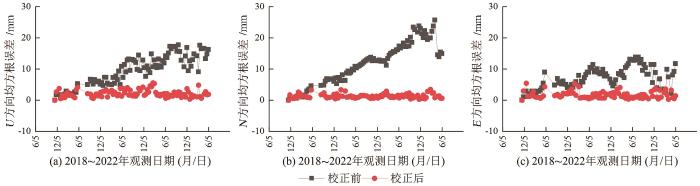
... 由图5可知,GNSS视线向形变量呈周期性变化,InSAR视线向形变量周期性较弱.InSAR和GNSS监测曲线的方向大致相同[37],但仍存在一些点位的InSAR和GNSS监测结果有明显差距,如5号、6号和18号点.这些点位可能是由于SAR卫星轨道误差、大气延迟等误差影响,导致与同期GNSS监测结果有差距.为了对InSAR观测值进行校正,在研究区同期观测的13个GNSS站中均匀选择7个GNSS点位作为先验点参与模型解算,剩余6个点位参与精度评定.如图6所示,黑色曲线表示InSAR视线向累积形变值,红色曲线表示投影到LOS方向的GNSS累积形变值,蓝色曲线表示经校正后InSAR累积形变值. ...
多时相Sentinel-1A InSAR的连盐高铁沉降监测分析
1
2021
... 由图5可知,GNSS视线向形变量呈周期性变化,InSAR视线向形变量周期性较弱.InSAR和GNSS监测曲线的方向大致相同[37],但仍存在一些点位的InSAR和GNSS监测结果有明显差距,如5号、6号和18号点.这些点位可能是由于SAR卫星轨道误差、大气延迟等误差影响,导致与同期GNSS监测结果有差距.为了对InSAR观测值进行校正,在研究区同期观测的13个GNSS站中均匀选择7个GNSS点位作为先验点参与模型解算,剩余6个点位参与精度评定.如图6所示,黑色曲线表示InSAR视线向累积形变值,红色曲线表示投影到LOS方向的GNSS累积形变值,蓝色曲线表示经校正后InSAR累积形变值. ...