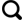1 引 言
地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] 。目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] 。然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h。由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性。故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制。因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献。
为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度。国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化。若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化。但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] 。固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化。静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少。2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机。
基于以上国内外的研究现状及存在的问题,利用FY-4A LST数据,引入地表温度日变化模型(DTC),构建基于日变化信息的LST时间归一化模型(Temporal-effect Normalization Model of land surface temperature Based on Diurnal variation information, BDTNM),对MODIS LST 数据进行时间归一化,以进一步提升MODIS LST 产品应用的精度和价值。
2 研究区与数据
2.1 研究区
研究区位于黑河流域中游的张掖地区(38°44′~38°59′ N,100°15′~100°34′E)。该地区位于甘肃省西北部,夹于祁连山脉、龙首山和合黎山之间,黑河流经此域,形成了特有的荒漠绿洲景象。核心实验区主要位于张掖绿洲及周边地区,地表覆盖类型主要包括建筑、农田、湿地、戈壁、荒漠和沙漠,其中绝大部分区域为农田,是典型的灌溉农业区。实验区地势平坦开阔,非常适合地表温度相关的研究,实验区位置范围及站点位置如图1 所示。其中,大满超级站、黑河遥感站、张掖湿地站的下垫面类型分别是玉米地、人工草地、芦苇湿地。
图1
图1
研究区范围及地面站点位置 审图号:GS(2020)4619
Fig.1
Location of the study area and each ground station
2.2 数据及预处理
研究所用的数据集有4种:FY-4A的LST产品数据集(FY4A_AGRI_L2_LST)、MODIS的每日陆地温度发射率产品数据集(MOD11B1/MYD11B1)、MODIS的LST产品数据集(MOD11A1/MYD11A1)和地面气象站点实测数据。数据的获取时间为2019年9月份。
(1)FY4A_AGRI_L2_LST数据集。下载自风云卫星遥感数据服务网(http:∥satellite.nsmc.org.cn/PortalSite/Default.aspx),并根据其提供的FY-4A数据行列号和经纬度互换方法,对数据集进行裁剪,获取覆盖研究区的FY-4A地表温度数据集。
(2)MOD11A1和MYD11A1地表温度和比辐射率产品,来自于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/)。本研究从MOD11A1和MYD11A1产品[9 -10 ] 中提取LST、卫星过境时间和质量控制数据。其中如图2 所示,各像元的局地太阳时显示出明显的分界线,导致LST在分界处存在突变,且存在部分空值。
图2
图2
研究区MODIS地表温度数据及过境时间
Fig.2
MODIS LST datasets and transit time in the research area
(3)MODIS的每日陆地温度发射率产品数据集(MOD11B1/MYD11B1),下载于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/)。该产品时空分辨率分别为每天6 km,对数据集中的20、22、23、29、31、32波段的发射率进行合成[11 -12 ] ,得到地面气象观测站点对应像元的宽波段发射率。
(4)地面气象站点实测数据。使用该数据集中的上下行长波辐射以及由步骤(3)估算的MODIS宽波段发射率集,基于Stefan-Boltzmann定律计算3个气象站点的地表温度[13 ] 。获取的地表温度以验证FY4A_AGRI_L2_LST产品空值插补精度、BDTNM模型的时间归一化精度和MODIS LST产品时间归一化精度,从而评估BDTNM模型的时间归一化性能。该数据集由寒区旱区科学数据中心(http:∥westdc.westgis.ac.cn/zh-hans/)提供。
3 研究方法
为了解决现有方法对MODIS LST数据时间归一化时所需辅助数据多、或模型受限于MODIS日内有效观测次数等问题,在静止卫星地表温度日变化模型的基础上,面向MODIS LST数据,提出一种基于地表温度日变化信息的地表温度时间归一化方法(BDTNM)。
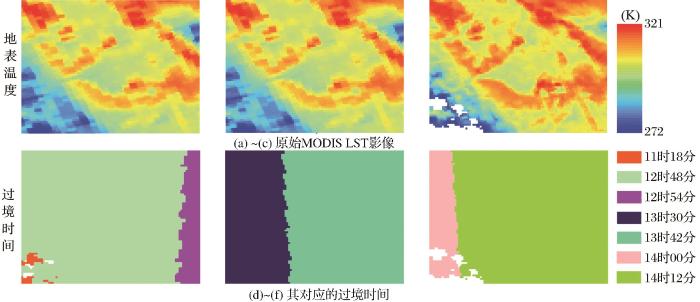
首先对FY-4A LST产品进行质量筛选,对空值采用顾及时空特征的FY-4A地表温度重建模型进行重建,并利用FY-4A数据建立适用于粗分辨率像元的DTC模型,得到FY-4A像元在MODIS真实过境时刻tr 和归一化时刻tp 的地表温度值;其次通过临近天时间窗口内的FY-4A和MODIS在tr 时刻的地表温度拟合粗细分辨率像元对应的转换系数;最后利用tp 时刻FY-4A的地表温度值和求得的转换系数加以计算,由此得到归一化时刻tp 时MODIS像元的地表温度,实现对MODIS地表温度的时间归一化,技术路线如图3 所示。
图3
图3
技术路线图
Fig.3
Technology roadmap
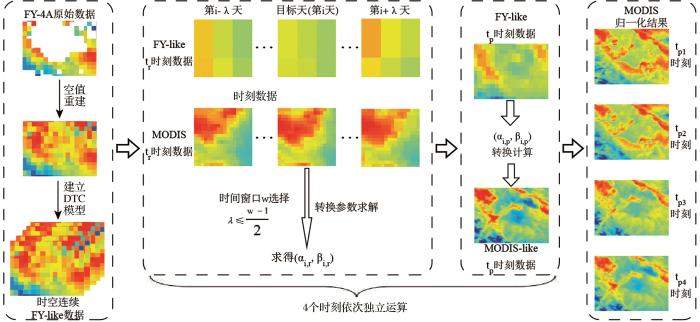
图4 展示了研究区内9月份MODIS LST产品过境时间的分布情况,本研究选择过境时间频率最高的邻近的整点时刻(北京时间3点、12点、14点、23点)作为归一化时刻。
图4
图4
MODIS LST数据过境时间频率分布图
Fig.4
MODIS LST data transit time frequency distribution
3.1 FY-4A LST产品空值填补方法
FY-4A的LST数据集在时空上具有一定的缺失,统计2019年9月的1 189幅FY-4A LST数据缺失情况,发现有效LST数据比例均值为46.24%,不同像元LST时序数据的有效率空间分布如图5 所示。因此需要对FY-4A的LST数据进行空值插补。
图5
图5
FY-4A LST数据时序有效率空间分布图
Fig.5
Spatial distribution of time efficiency of FY-4A LST dataset
研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建。即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补。选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建。最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建。
3.2 FY-4A LST的DTC模型建立
经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] 。孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度。故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息。具体为:
T 1 ( t ) = T 0 + T a c o s ( β ( t - t m ) ) t < t s T 2 ( t ) = b 1 + b 2 e α ( t - t s ) t ≥ t s 其中 : b 2 = - β T a s i n ( β ( t s - t m ) ) / α b 1 = T 0 + T a c o s ( β ( t s - t m ) ) - b 2 (1)
其中:T1 /T2 为是模型中分别代表白天/夜晚温度的两个部分,其中t 是时间,T0 是日出前后的残余温度,Ta 是温度振幅,tm 是温度到达最大值的时间,ts 是温度开始自由衰减的时间,α 是地表温度的衰减系数,β 是角频率。
使用空值填补后的一日内n 个FY⁃4A LST数据,依据Duan等的研究[4 ,15 ] 设置模型参数的初值,采用Levenberg-Marquardt非线性最小二乘方法进行拟合计算得到了每个像元适用于FY⁃4A的6个参数的值(式(2)),由此,得到FY⁃4A每个像元的地表温度日变化曲线(式(3)):
T 0 F Y - 4 A , d , T a F Y - 4 A , d , t m F Y - 4 A , d , t s F Y - 4 A , d , α F Y - 4 A , d , β F Y - 4 A , d = f T F Y - 4 A , d , t 1 , t r 1 , ⋯ ⋯ , T F Y - 4 A , d , t n , t r 4 (2)
L S T F Y - 4 A ( t , d ) = D T C ( T 0 F Y - 4 A , d , T a F Y - 4 A , d , t m F Y - 4 A , d , t s F Y - 4 A , d , α F Y - 4 A , d , β F Y - 4 A , d , t ) (3)
其中:T 0 F Y - 4 A , d T a F Y - 4 A , d t m F Y - 4 A , d t s F Y - 4 A , d α F Y - 4 A , d β F Y - 4 A , d T F Y - 4 A , d , t 1 L S T F Y - 4 A ( t , d )
3.3 归一化时刻MODIS地表温度求解
不同卫星传感器(MODIS和FY⁃4A)由于尺度效应及成像方式等不同,获取的地表温度有差异,二者之间存在一定转换关系,MODIS LST产品在短时间内的变化值Δ T M O D I S d i , t Δ T F Y - 4 A d i , t η (式(4)):
Δ T M O D I S d i , t = η * Δ T F Y - 4 A d i , t (4)
下垫面类型不是均质时,16个细分辨率像元(MODIS,1 km)与其空间对应的1个粗分辨率像元(FY-4A,4 km)进行转换时,每个像元的转换系数不同,不能仅用一个参数来定义两者间的转换。这里引入m 和q 分别作为细分辨率像元与对应的粗分辨率像元的转换系数中的乘常数和加常数(式(5)),以此解决非均质地表的混合像元的粗细分辨率LST的转换问题。
T M O D I S d i , t k = m i , k * T F Y - 4 A d i , t k + q i , k (5)
其中:T M O D I S d i , t k T F Y - 4 A d i , t k mi,k 和qi,k 分别是第i天k时刻细分辨率像元与对应的粗分辨率像元的转换系数中的乘常数和加常数。
地表温度在短时间内的变化是可以看作是线性的[23 ] ,可以认为不同空间分辨率的LST之间的关系在短时间内是相似恒定的,即认为短时间内m 和q 不会变化。
l i m t b - t a → 0 m i , a = m i , b = η , l i m t b - t a → 0 q i , a = q i , b (6)
另外,我们又认为在临近天内这种转换关系是相似的,即同一像元在临近天内有一致的转换系数,因此可以通过对目标像元在临近天内开时间窗口w 的方式,来拟合求解转换系数值。以此求得每个细分辨率像元对应的转换系数m 和q 。
T M O D I S d i , t k = m i , k * T F Y - 4 A d i , t k + q i , k (7)
T M O D I S d i ± 1 , t k = m i ± 1 , k * T F Y - 4 A d i ± 1 , t k + q i ± 1 , k (8)
T M O D I S d i ± λ , t k = m i ± λ , k * T F Y - 4 A d i ± λ , t k + q i ± λ (9)
m i , k , q i , k = m i ± 1 , k , q i ± 1 , k = ⋯ ⋯ = m i ± λ , k , q i ± λ , k λ ≤ w - 1 2 (10)
m i , k , q i , k = f ( T M O D I S d , t k , T M O D I S d i ± 1 , t k , ⋯ ⋯ , T M O D I S d i ± λ , t k , T F Y - 4 A d , t k , T F Y - 4 A d i ± 1 , t k , ⋯ ⋯ , T F Y - 4 A d i ± λ , t k ) 其中 : T F Y - 4 A d i , t k = L S T F Y - 4 A ( t k , d i ) = D T C ( T 0 F Y - 4 A , d i , T a F Y - 4 A , d i , t m F Y - 4 A , d i , t s F Y - 4 A , d i , α F Y - 4 A , d i , β F Y - 4 A , d i , t k ) (11)
于是,归一化时刻t p 处的MODIS地表温度T M O D I S d i , t k
T M O D I S d i , t p = m i , p * T F Y - 4 A d i , t p + q i , p (12)
其中:由于归一化时刻tp 与真实过境时刻tr 临近,根据式(6)的假设,本研究令:
m i , p , q i , p = m i , r , q i , r (13)
T M O D I S d i , t p = m i , r * T F Y - 4 A d i , t p + q i , r = m i , r * L S T F Y - 4 A ( t p , d i ) + q i , r (14)
其中:4个时刻的归一化过程均为独立运算,MODIS一日内的4次观测数据互相不参与运算。
3.4 精度评价指标
将黑河中游流域的MODIS LST产品归一化至北京时间的3点、12点、14点、23点并插补至无缝。利用地面站点实测的地表温度,采用皮尔逊相关系数r(Pearson Correlation Coefficient)、均方根误差RMSE(Root-Mean Squared Error)和平均绝对误差MAE(Mean Absolute Error)作为评价指标,来验证模型对FY-4A LST的空值插补以及对MODIS LST时间归一化的精度。其次,本研究为了探求时间窗口w 的大小对模型的影响,将窗口大小定义为2~9 d,来探求最合适的时间窗口大小。此外,本研究还与直接使用MODIS数据建立4参数DTC(INA08_2模型)进行时间归一化的方法进行了比较。为了消除MODIS本身精度对方法精度的检验,还将MODIS真实过境时刻tr 时的站点数据用两种方法归一化至tp 时刻,对比其结果的精度。并用模拟数据探求了BDTNM模型对MODIS数据的空值插补能力。
4 结果与分析
4.1 FY-4A空值插补结果
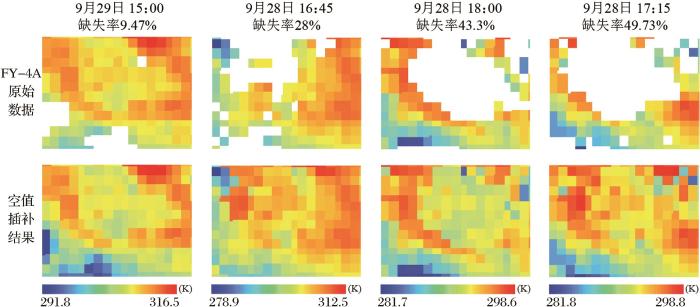
图6 为2019年FY-4A LST不同缺失率的重建结果,由图6 可知,无论是空间缺失率高还是低的LST数据,本研究提出的模型均可以插补至无缝,插补结果几乎没有异常值,且没有斑块效应。
图6
图6
FY-4A原始数据及空值插补后结果
Fig.6
FY-4A LST dataset before and after image reconstruction
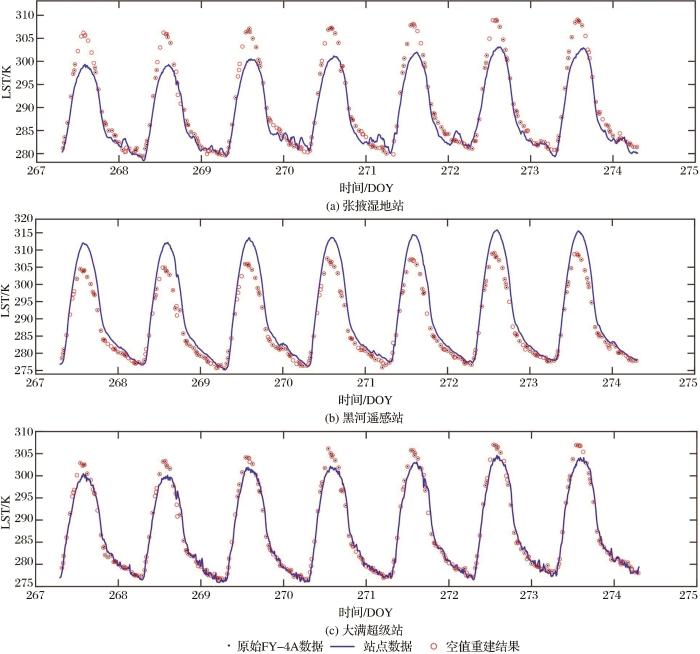
以黑河流域中游区域张掖湿地站(芦苇湿地)、黑河遥感站(人工草地)和大满超级站(玉米田)验证了对FY-4A LST数据空值的重建的精度,图7 展示了3个站点处的FY-4A的LST产品时序数据、站点实测数据以及重建后的LST时序数据。由LST随时间变化曲线可以看出,在每日的11点至16点,FY-4A数据与站点实测数据有较大差距,其中在张掖湿地站和大满超级站表现为FY-4A数据高估于站点数据,在黑河遥感站表现为FY-4A数据低估于站点数据,其他时刻差距较小;重建得到的数据与站点数据出现较大误差的时刻也是在每日11至16点,高估和低估情况与原始数据吻合。本方法保留了绝大部分原始FY-4A的LST数据,可以实现对无效LST值的重建,并且保留了FY-4A LST数据随时间变化的特征,得到的曲线平滑,没有异常波动。
图7
图7
FY-4A LST在站点处重建结果图
Fig.7
The reconstruction result of FY-4A LST at the sites
基于站点数据验证所得的2019年年积日(Day of Year, DOY)267-273的FY-4A原始及重建误差如表1 所示,其中FY-4A原始数据为去除无效像元后剩余的有效数据,重建后数据为原始有效数据和对无效像元重建得到的数据,仅重建部分为对无效像元重建得到的数据。在3个站点处的空值重建后的数据精度与原始精度相当(表1 ),RMSE增加小于1 K,因此,本方法可以在不改变原有的FY-4A LST产品精度的前提下,对于不同下垫面类型,都可以对FY-4A数据的缺失像元进行重建,得到无缝的FY-4A LST数据,以建立适用于FY-4A的DTC模型,进一步实现MODIS数据的时间归一化。
4.2 归一化时间窗口的确定
在求解粗细像元转换系数时,时间窗口大小,对归一化结果的精度。在BDTNM模型实验中,时间窗口设置为2~9 d,步长为1 d,当时间窗口大小为偶数时,选取目标像元前序像元比后序像元多一个。当其他因素固定时,随着时间窗口的增加,RMSE和MAE先降低后平稳并略微增加,当时间窗口大小为7 d时,归一化精度相对最高(表2 )。这是由于当参与拟合计算的像元数过少时,方程稳定性降低,容易受到天气波动数据质量等因素影响;而参与拟合的像元数目增多时,参与拟合的LST与目标天的LST之间的相关性随间隔日期增大而降低,且之间的MODIS卫星过境时间差也可能增大,导致拟合方程中误差项增多,精度降低。
4.3 基于站点地表温度的时间归一化结果验证
研究使用BDTNM模型对DOY267-273内28次过境的MODIS数据进行了时间归一化;并将INA08模型[24 ] 参数ts 固定为日落时间tss 前一小时,使用MODIS一日4次的数据建立INA08_2模型,对MODIS LST数据进行时间归一化[4 ] 。利用研究区内3个站点的实测数据对两种方法的归一化结果进行精度评价。
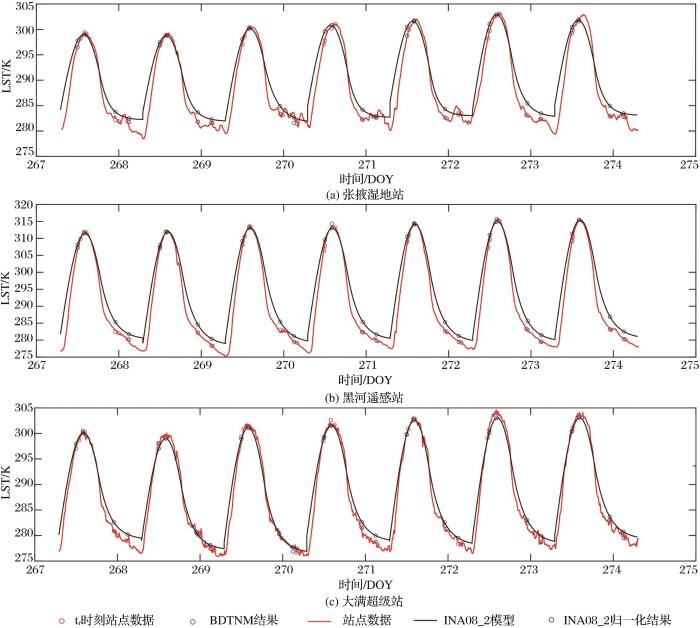
图8 展示了7 d内3个站点处的MODIS LST产品时序数据、两种方法的归一化结果和站点实测数据。可以看出,与站点实测数据对比,白天两次过境的MODIS LST数据在张掖湿地站和大满超级站略有高估,在黑河遥感站表现出较大的低估,夜晚差距不大。两种方法对MODIS LST数据进行时间归一化时均保留了MODIS数据的特性,没有明显的异常值,但在黑河遥感站,MODIS LST数据及归一化结果与站点实测数据表现出较大差距。
图8
图8
两种方法在站点处时间归一化结果图(MODIS LST)
Fig.8
The temporally normalized result of two methods at sites (MODIS dataset)
由表3 可得,在张掖湿地站和大满超级站,MODIS LST数据的RMSE和MAE均在1 K左右,两种归一化方法归一化结果的RMSE和MAE增加均在1 K以内,其中BDTNM模型优于INA08_2模型0.4 K左右;在黑河遥感站处,INA08_2模型和BDTNM的归一化结果的RMSE分别为5.41 K和5.25 K,这是因为MODIS LST数据的RMSE已大于5 K,MODIS LST和站点实测数据之间存在一定的系统偏差。
因此,使用BDTNM法对MODIS数据进行时间归一化,不仅保留了MODIS数据的特性,维持了MODIS数据本身的精度,还具有较INA08_2模型更好的模型精度。
4.4 基于模拟数据的时间归一化结果验证
由于MOIDS数据与站点数据之间存在一定的系统偏差,会对归一化结果的精度验证造成影响,又因为INA08_2模型方法以及BDTNM模型并没有使用到MODIS LST数据空间域的领域信息,为了消除4.3节中提到的系统偏差,本研究将DOY 267~273共7 d的站点数据作为模拟数据,在3个站点处分别采用INA08_2模型和BDTNM模型将MODIS真实过境时刻tr 时的站点数据归一化至tp 时刻,与tp 时刻的站点数据进行比较,评价两种方法的归一化精度。
由图9 可知,尽管INA08_2已经是4参数DTC模型中拟合精度和鲁棒性较好的半经验模型,但在这3个站点中均表现出在12~16点拟合精度最高、夜晚拟合精度不佳的现象,在MODIS夜晚的两次过境时刻,INA08_2模型仅在大满超级站表现出较好的归一化结果,在张掖湿地站与黑河遥感站,时间归一化的结果与真实数据有较大差距。 而BDTNM模型对站点实测数据的归一化结果在3个站点的4个时刻均表现一致,无明显的异常值。
图9
图9
两种方法站点处时间归一化结果图(模拟数据)
Fig.9
The temporally normalized result of two methods at sites (analog dataset)
模拟数据时间归一化误差如表4 所示,其中未做归一化通过真实过境时刻tr 时的站点地表温度与归一化时刻tp 时的站点地表温度计算得来,即若不做时间归一化,用tr 时刻的地表温度来代替tp 时刻的地表温度,则导致RMSE 1 K左右、MAE 0.7 K左右的误差。使用INA08_2模型进行时间归一化,RMSE和MAE大于1 K;使用BDTNM模型进行时间归一化,RMSE为0.46 K、MAE为0.32 K,其中效果最好为黑河遥感站,效果较差是张掖湿地站。表明BDTNM模型能够较好地对地表温度数据进行时间归一化。其中,黑河遥感站的下垫面类型为草地,每天的温度波动较大,故未做归一化引起的误差在该站最大,而INA08模型本身描述日内温度变化信息的精度就不如其他的六参数DTC模型,且在草地裸地或稀疏植被这两种地表覆盖类型的拟合精度最差[21 ] ,因此,INA08_2模型时间归一化在黑河遥感站精度最低;由于FY-4A具有高时间分辨率,足够的观测量可以更加全面地观测到一日内的温度变化,且JNG06模型也具有较好的拟合精度,因此BDTNM模型在张掖湿地站表现出很好的精度。另外,两种方法均在大满超级站(玉米田)的精度均高于张掖湿地站(芦苇湿地),这是由于地表温度日变化模型在农用地具有最好的拟合精度[21 ] 。其中,BDTNM是不同站点之间精度差异较小,这是由于粗细像元之间的转换系数求解的精度几乎不受下垫面类型的影响。综上所述,BDTNM模型对地表温度的时间归一化的精度受下垫面类型的影响较小。
另外,INA08_2模型和BDTNM模型归一化的结果在4个归一化时刻呈现一定的差异(表5 )。研究日期以晴天为主,中午14时天气状况更好,受云、风等影响较少,DTC模型在这个时刻展现出更好的拟合精度,而夜晚,尤其两日的交接处,DTC模型存在较大的拟合误差,因此INA08_2模型的时间归一化结果白天精度高于夜晚;相较于INA08_2模型仅能在14点获得较好的归一化精度,BDTNM模型能在各个时刻均表现出良好的精度,而在张掖湿地站的3点时刻,BDTNM模型精度最低,这是由于该站点在凌晨0点至8点之间,温度波动较大(图9 (c)),造成DTC模型拟合精度较低,增大tp1 时刻粗像元LST的误差,导致求解的tp1 时刻的MODIS LST值出现偏差,因此BDTNM模型在这里精度较低。
4.5 模型适用性分析
4.5.1 MODIS LST产品空值对时间归一化的影响
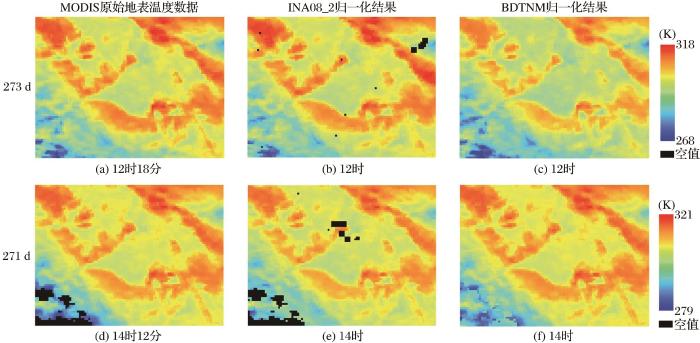
图10 中(a)、(d)为试验区的MODIS LST数据,(b)和(c)、(e)和(f)分别是INA08_2模型和BDTNM模型对(a)、(d)的时间归一化结果图。
图10
图10
研究区MOIDS数据及两种方法时间归一化结果图
Fig.10
The MODIS temporally normalization result of two methods in the research area
INA08_2模型对DOY273的tr2 时刻MODIS LST影像时间归一化时,由于tr1 时刻存在无效像元导致其对应的tr2 时刻像元无法完成归一化(图10 (b));而无论参与拟合的原始数据是否有空值,BDTNM模型的时间归一化的结果均没有空值。造成上述现象的原因是INA08_2模型在对MODIS LST某空间像元进行时间归一化时要求日内四次观测均为有效值,故若该空间像元日内4次观测出现空值,则4次观测均无法完成时间归一化;而BDTNM由于其模型自身的优势,在对目标时刻的像元进行归一化时,精度不受日内其他3次观测的缺值与否、观测质量等的影响;若出现因云遮档、数据质量等引起的MODIS数据缺失,导致目标像元为无效像元,BDTNM模型可以根据空间像元时间窗口内临近天的MODIS LST数据和FY-4A LST数据求解粗细分辨率像元间的转换系数,并利用目标像元对应的FY-4A LST数据完成对空值的重建,并归一化至标准时刻。但由于细分辨率像元的数据缺失,会在转换系数的求解时缺少约束项,从而带来误差,为了探求该误差的大小,本研究利用DOY267-273共7 d的站点数据作为模拟数据,模拟了在临近天数据无缺失的情况下,将目标时刻tr 时的像元做空值处理,利用BDTNM模型将目标像元(空值)归一化至tp 时刻,与tp 时刻的站点数据做对比来验证精度。
如表6 所示,BDTNM模型可以将这种情况的缺值完成填补并归一化, RMSE为0.53 K,MAE为0.48 K同比无缺值的情况归一化误差增加了0.2 K以内,其中,BDTNM在14时表现出最好的填补精度,这是因为,地表温度在14时左右变化趋势最小,临近天变化规律恒定,缺少当天像元对BDTNM模型的影响最低。总体来说,BDTNM可以完成在MODIS数据出现空值,并且该空值像元临近天同一时刻有值的情况下,对MODIS数据的插补及时间归一化。
4.5.2 时间差对归一化结果的影响
本研究统计了研究区9月MODIS LST数据的过境时间与归一化时刻的差值大小,其中,小于0.5 h的占比54.85%,大于等于0.5 h、小于1 h的占比41.63%,大于等于1 h、小于1.5 h的占比3.36%,大于等于1.5 h、小于2 h的占比0.16%.
为了探求MODIS过境时间与归一化时刻差值大小对时间归一化精度的影响以及式13的合理性,本研究利用DOY267~273共7 d的站点实测数据作为模拟数据,将4个时间差值段内的所有数据利用INA08_2模型和BDTNM模型分别归一化至标准时刻,并验证了结果的精度。
如表7 所示,与标准时刻之间的时间差值越大,LST的差异越大。使用INA08_2模型和BDTNM模型进行时间归一化时,在时差大小为0.5 h内时精度最高,在时差大小为1.5~2 h时精度最低。两种方法在进行时间归一化时都呈现出精度谁时间差值增大而减小的现象,但总体来看,两种方法的精度下降都较小,这也验证了式(13)的合理性。且在各时差段,BDTNM模型的精度都优于INA08_2模型。由此可得,BDTNM模型可以对所有过境时刻的MODIS LST数据高精度地归一化至标准时刻。
5 结 论
地表温度随时间快速变化,且极轨卫星遥感获取到的LST在像元间局地太阳时存在差异,导致空间上不同像元之间以及空间上同一像元不同天之间缺乏可比性,一般需要时间归一化之后才能提高实际使用价值。本研究以张掖地区为研究区域,针对4参数DTC模型(INA08_2)对MODIS地表温度数据时间归一化精度不高、且在日内数据有缺失的情况下无法建立模型进行时间归一化等问题,建立了面向MODIS LST产品的基于地表温度日变化信息的时间归一化方法。利用站点数据,对INA08_2模型和BDTNM模型时间归一化结果进行了验证和评价。
据张掖地区DOY267-273站点数据表明,忽略MODIS像元间局地太阳时的差异,直接使用LST数据会带来造成RMSE 1 K左右、MAE 0.7 K左右的误差,使用INA08_2模型和BDTNM模型对LST进行时间归一化可以减小这个误差,进而得到较大范围时间一致的LST数据。BDTNM还有以下特点:①BDTNM模型可以实现对不同缺失率的FY-4A LST数据进行无缝重建,以建立高精度的FY-4A DTC模型。②BDTNM模型的时间归一化结果在时间尺度变化趋势上更贴近MODIS特征、与实际情况更加吻合,归一化后的MODIS LST数据的RMSE为2.61 K、MAE为2.09 K,相较于原始MODIS数据(RMSE 2.62 K、MAE 2.08 K)归一化结果对MODIS LST的改变较小。③利用模拟数据进行实验并评价,结果表明,BDTNM模型时间归一化精度(RMSE 0.45 K、MAE 0.32 K)高于INA08_2模型(RMSE 1.36 K、MAE 1.15 K);且BDTNM模型归一化精度受下垫面类型、归一化时刻、归一化时间大小影响较小。④BNDTM模型对MODIS LST某一时刻观测数据进行时间归一化时,不需要借助其他3个时刻观测的结果,且有对MODIS LST数据的空值重建的能力。依据模拟数据验证,MODIS LST数据空值对BDTNM模型的影响在0.2 K以内。
本模型存在以下不足:①面对连续多天阴雨的情况,FY-4A LST空值重建的精度会有所下降,导致BDTNM模型整体精度下降。②虽然本文针对黑河中游地区及站点验证表明BDTNM模型中时间窗口大小为7天时效果最好,但对于其他地区,仍需要试验讨论,确立合适的时间窗口大小,才可大范围应用。
参考文献
View Option
[1]
YANG Yingbao LI Xiaolong CAO Chen Downscaling urban land surface temperature based on multi-scale factor
[J]. Science of Surveying and Mapping ,2017 ,42 (10 ):73 -79 .
[本文引用: 1]
杨英宝 ,李小龙 ,曹晨 多尺度城市地表温度降尺度方法
[J].测绘科学 ,2017 ,42 (10 ):73 -79 .
[本文引用: 1]
[2]
ZHAO Wei LI Ainong ZHANG Zhengjian et al A Study on land surface temperature terrain effect over mountainous area based on Landsat 8 thermal infrared data
[J]. Remote Sensing Technology and Application ,2016 ,31 (1 ):63 -73 .
[本文引用: 1]
赵伟 ,李爱农 ,张正健 ,等 基于Landsat 8热红外遥感数据的山地地表温度地形效应研究
[J].遥感技术与应用 ,2016 ,31 (1 ):63 -73 .
[本文引用: 1]
[3]
ZHOU J DAI F N ZHANG X D et al Developing a Temporally Land Cover-Based Look-Up Table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass
[J]. International Journal of Applied Earth Observation and Geoinformation ,2015 ,34 :35 -50 .DOI: 10.1016/j.jag.2014.07.001
[本文引用: 1]
[4]
DUAN Sibo Methodology development for temporal normalization of land surface temperature product derived from polar-orbiting satellite data
[D]. Beijing :Chinese Academy of Sciences ,2014 .
[本文引用: 3]
段四波 极轨卫星地表温度产品的时间归一化方法研究
[D]. 北京 :中国科学院研究生院 ,2014 .
[本文引用: 3]
[5]
ZHAO W WU H YIN G et al Normalization of the temporal effect on the MODIS land surface temperature product using random forest regression
[J]. ISPRS Journal of Photogrammetry & Remote Sensing ,2019 ,152 :109 -118 . DOI:10.1016/j.is-prsjprs.2019.04.008
[本文引用: 1]
[6]
DUAN S B LI Z L TANG B H et al Generation of a time-consistent land surface temperature product from MODIS data
[J]. Remote Sensing of Environment ,2014 ,140 (140 ):339 -349 .DOI: 10.1016/j.rse.2013.09.003
[本文引用: 1]
[7]
DUAN S B LI Z L TANG B H et al Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from Clear-Sky MODIS data
[J]. Remote Sensing , 2014 , 6 (4 ):3247 -3262 . DOI: 10.3390/rs6043247
[本文引用: 1]
[8]
ZHU Linqing ZHOU Ji LIU Shaomin et al Temporal normalization research of airborne land surface temperature
[J]. Journal of Remote Sensing ,2017 ,21 (2 ):193 -205 .
[本文引用: 1]
朱琳清 , 周纪 , 刘绍民 ,等 航空遥感地表温度时间归一化
[J]. 遥感学报 ,2017 ,21 (2 ):193 -205 .
[本文引用: 1]
[9]
WAN Z DOZIER J A generalized split-window algorithm for retrieving land-surface temperature from space
[J]. IEEE Transactions on Geoscience & Remote Sensing ,1996 ,34 (4 ):892 -905 .
[本文引用: 1]
[10]
MAO Kebia QIN Zhihao SHI Jiancheng et al The research of split-window algorithm on the MODIS
[J]. Geomatics and Information Science of Wuhan University , 2005 ,30 (8 ): 703 -707 .
[本文引用: 1]
毛克彪 ,覃志豪 ,施建成 ,等 针对MODIS影像的劈窗算法研究
[J]. 武汉大学学报·信息科学版 , 2005 ,30 (8 ): 703 -707 .
[本文引用: 1]
[11]
SNYDER W C WAN Z ZHANG Y et al Thermal infrared(3~14 μm) bidirectional reflectance measurements of sands and soils
[J]. Remote Sensing of Environment ,1997 ,60 (1 ):101 -109 .DOI: 10.1016/S0034-4257(96)00166-6
[本文引用: 1]
[12]
SNYDER W C WAN Z BRDF models to predict spectral refle-ctance and emissivity in the thermal infrared
[J]. IEEE Tran-sactions on Geoscience & Remote Sensing ,1998 ,36 (1 ):214 -225 . DOI:10.1109/36.655331
[本文引用: 1]
[13]
YANG Y CAO C PAN X et al Downscaling land surface temperature in an arid area by using multiple remote sensing indices with random forest regression
[J]. Remote Sensing , 2017 , 9 (8 ): 789 -795 . DOI: 10.3390/rs9080789
[本文引用: 1]
[14]
WANG Aihui YANG Yingbao PAN Xin et al Land surface temperature reconstruction model of FY ‐4A cloudy pixels considering spatial and temporal characteristics
[J]. Geomatics and Information Science of Wuhan University ,2021 ,46 (6 ):852 -862 .
[本文引用: 1]
王爱辉 ,杨英宝 ,潘鑫 ,等 顾及时空特征的 FY‐4A 云覆盖像元地表温度重建模型
[J]. 武汉大学学报·信息科学版 ,2021 ,46 (6 ):852 -862 .
[本文引用: 1]
[15]
GAO F MASEK J SCHWALLER M et al On the blending of the landsat and MODIS surface reflectance: predicting daily landsat surface reflectance
[J]. IEEE Transactions on Geoscience and Remote Sensing ,2006 ,44 (8 ):2207 -2218 . DOI:10.1109/TGRS.2006.872081
[本文引用: 2]
[16]
ZHOU Yi QIN Zhihao BAO Gang Land surface temperature estimation under cloud cover with GIDS
[J]. Journal of Remote Sensing ,2012 ,16 (3 ):492 -504 .
[本文引用: 1]
周义 , 覃志豪 , 包刚 GIDS 空间插值法估算云下地表温度
[J]. 遥感学报 ,2012 ,16 (3 ): 492 -504 .
[本文引用: 1]
[17]
XUE Xingsheng WU Yanlan A comparison of missing data reconstruction methods for FengYun geostationary satellite land surface temperature products
[J]. Journal of Anhui Agricultural University ,2017 ,44 (2 ):308 -315 .
[本文引用: 1]
薛兴盛 ,吴艳兰 面向风云静止卫星地表温度产品的缺失数据修复方法对比
[J]. 安徽农业大学学报 ,2017 ,44 (2 ):308 -315 .
[本文引用: 1]
[18]
SAVITZKY A GOLAY M Smoothing and differentiation of data by simplified least squares procedures
[J]. Analytical Chemistry , 1964 , 36 (8 ): 1627 -1639 . DOI: 10.1021/ac60214a047
[本文引用: 1]
[19]
FANG Yingbo ZHAN Wenfeng HUANG Fan et al Hourly variation of surface urban heat island over the Yangtze River delta urban agglomeration
[J]. Advances in Earth Science ,2017 ,32 (2 ):187 -198 .
[本文引用: 1]
方迎波 ,占文凤 ,黄帆 ,等 长三角城市群表面城市热岛日内逐时变化规律
[J].地球科学进展 ,2017 ,32 (2 ):187 -198 .
[本文引用: 1]
[20]
DUAN S B LI Z L NING W et al Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satel-lite data
[J]. Remote Sensing of Environment ,2012 , 124 : 15 -25 .DOI: 10.1016/j.rse.2012.04.016
[本文引用: 1]
[21]
MENG Xiaocheng LIU Hao CHENG Jie Evaluation and characteristic research in diurnal surface temperature cycle in China using FY-2F data
[J]. Journal of Remote Sensing ,2019 ,23 (4 ):570 -581 .
[本文引用: 3]
孟翔晨 , 刘昊 , 程洁 2019 . 基于FY-2F数据的中国区域地表温度日变化模型评价及特征研究
[J]. 遥感学报 ,2019,23 (4 ):570 -581 .
[本文引用: 3]
[22]
JIANG G M LI Z L Nerry F Land surface emissivity retrieval from combined mid-Infrared and thermal infrared data of MSGSEVIRI
[J]. Remote Sensing of Environment ,2006 ,105 (4 ): 326 -340 .
[本文引用: 1]
[23]
ZHOU X YU Y et al Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States
[J]. Remote Sensing of Environment ,2018 ,206 :84 -97 . DOI:10.1016/j.rse.2017. 12.010
[本文引用: 1]
[24]
INAMDAR A K FRENCH A HOOK S et al Land surface temperature retrieval at high spatial and temporal resolutions over the Southwestern United States
[J]. Journal of Geophysical Research: Atmospheres ,2008 ,113 (D7 ):D07107 .DOI: 10.1029/2007jd009048
[本文引用: 1]
多尺度城市地表温度降尺度方法
1
2017
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
多尺度城市地表温度降尺度方法
1
2017
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
基于Landsat 8热红外遥感数据的山地地表温度地形效应研究
1
2016
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
基于Landsat 8热红外遥感数据的山地地表温度地形效应研究
1
2016
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
Developing a Temporally Land Cover-Based Look-Up Table (TL-LUT) method for estimating land surface temperature based on AMSR-E data over the Chinese landmass
1
2015
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
极轨卫星地表温度产品的时间归一化方法研究
3
2014
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
... 使用空值填补后的一日内n 个FY⁃4A LST数据,依据Duan等的研究[4 ,15 ] 设置模型参数的初值,采用Levenberg-Marquardt非线性最小二乘方法进行拟合计算得到了每个像元适用于FY⁃4A的6个参数的值(式(2) ),由此,得到FY⁃4A每个像元的地表温度日变化曲线(式(3) ): ...
... 研究使用BDTNM模型对DOY267-273内28次过境的MODIS数据进行了时间归一化;并将INA08模型[24 ] 参数ts 固定为日落时间tss 前一小时,使用MODIS一日4次的数据建立INA08_2模型,对MODIS LST数据进行时间归一化[4 ] .利用研究区内3个站点的实测数据对两种方法的归一化结果进行精度评价. ...
极轨卫星地表温度产品的时间归一化方法研究
3
2014
... 地表温度(Land Surface Temperature,LST)决定了地表辐射能量平衡中的长波辐射,能够提供地表能量平衡状态的时空变化信息,是气候、水文、生态和生物地球化学模式以及数据同化的关键参量,在探究地球面水和能量平衡方面发挥着重要作用[1 -2 ] .目前,热红外遥感是获取区域尺度地表温度信息的一种有效方法[3 ] .然而,遥感获取的地表温度信息是卫星过境时刻的瞬时值,且由于极地轨道卫星MODIS缺乏保持太阳同步轨道的主动控制器及其仪器具有固有的扫描特性,在一条MODIS扫描线上的同一次过境的不同像元或者在MODIS一个重返周期内不同天的同一像元的局地太阳时差值高达2 h.由于地表温度随局地太阳时变化,不同下垫面的地表温度变化率可以达到2 K/h至5 K/h,致使同一天不同像元或者同一像元不同天的地表温度产品之间缺乏可比性[4 ] ,直接将MODIS LST应用于大面积或长时序的研究(如估计地表土壤水分和能量通量)时,将会产生一定的不确定性.故即使地表温度被高精度地反演出来,其应用价值也会因为卫星过境像元之间局地太阳时存在差异而受到极大的限制.因此,对MODIS地表温度产品做时间归一化,提高地表温度产品之间的区域可比性和时序可比性,不仅可增强地表温度产品在全球气候变化分析中的实用价值,而且可为地表温度定量遥感反演研究做出积极的贡献. ...
... 使用空值填补后的一日内n 个FY⁃4A LST数据,依据Duan等的研究[4 ,15 ] 设置模型参数的初值,采用Levenberg-Marquardt非线性最小二乘方法进行拟合计算得到了每个像元适用于FY⁃4A的6个参数的值(式(2) ),由此,得到FY⁃4A每个像元的地表温度日变化曲线(式(3) ): ...
... 研究使用BDTNM模型对DOY267-273内28次过境的MODIS数据进行了时间归一化;并将INA08模型[24 ] 参数ts 固定为日落时间tss 前一小时,使用MODIS一日4次的数据建立INA08_2模型,对MODIS LST数据进行时间归一化[4 ] .利用研究区内3个站点的实测数据对两种方法的归一化结果进行精度评价. ...
Normalization of the temporal effect on the MODIS land surface temperature product using random forest regression
1
2019
... 为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度.国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化.若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化.但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] .固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化.静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少.2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机. ...
Generation of a time-consistent land surface temperature product from MODIS data
1
2014
... 为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度.国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化.若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化.但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] .固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化.静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少.2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机. ...
Estimation of diurnal cycle of land surface temperature at high temporal and spatial resolution from Clear-Sky MODIS data
1
2014
... 为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度.国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化.若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化.但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] .固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化.静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少.2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机. ...
航空遥感地表温度时间归一化
1
2017
... 为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度.国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化.若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化.但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] .固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化.静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少.2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机. ...
航空遥感地表温度时间归一化
1
2017
... 为了消除这种影响,国内外很多学者做了针对MODIS LST产品归一化的研究,主要可分为以下两类:一是将短时间内的地表温度变化看作线性变化,利用DEM(Digital Elevation Model)、NDVI(Normalized Difference Vegetation Index)、EVI(Enhanced Vegetation Index)等辅助数据求其线性变化的斜率,得到短时间内温度的变化量,累积至归一化时刻,求得归一化时刻的地表温度[5 -6 ] ,这类方法需要一些辅助数据(如NDVI、DEM、EVI等);另一种则是根据热传导方程或者能量平衡方程,建立地表温度日变化模型(Diurnal Temperature Cycle, DTC),来求得归一化时刻的地表温度.国内外研究者已经发展了许多地表温度日变化模型,这些模型分别采用不同的数学形式和模型参数描述地表温度日变化.若能通过已有数据,拟合出DTC模型建立所需参数,则能通过DTC模型预测任何时刻的地表温度,并可用于对遥感地表温度进行时间归一化.但由于极轨卫星时间分辨率不高,观测频率有限,日内观测次数小于DTC模型参数个数,导致无法成功拟合出所需参数,因此往往采用固定某个参数[7 ] 或添加地面站点获取的气象数据的方法[8 ] .固定某个参数的方法虽然已将DTC模型的参数简化至4个(如GOT01_0、INA08_2模型等),但当云雨天气影响,MODIS数据出现空值,即某空间像元日内有效观测数目小于4次时,则因无法建立DTC模型导致无法进行时间归一化.静止轨道气象卫星具有高时间分辨率的特征,日内观测次数能够满足DTC模型参数拟合的需求,但目前考虑借助静止卫星高时间分辨率来对极轨卫星做时间归一化的研究还较少.2016年12月发射的FY-4A是第二代对地静止轨道气象卫星,FY-4A卫星的成功发射为获得地表温度的日变化信息提供了新的契机. ...
A generalized split-window algorithm for retrieving land-surface temperature from space
1
1996
... (2)MOD11A1和MYD11A1地表温度和比辐射率产品,来自于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/).本研究从MOD11A1和MYD11A1产品[9 -10 ] 中提取LST、卫星过境时间和质量控制数据.其中如图2 所示,各像元的局地太阳时显示出明显的分界线,导致LST在分界处存在突变,且存在部分空值. ...
针对MODIS影像的劈窗算法研究
1
2005
... (2)MOD11A1和MYD11A1地表温度和比辐射率产品,来自于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/).本研究从MOD11A1和MYD11A1产品[9 -10 ] 中提取LST、卫星过境时间和质量控制数据.其中如图2 所示,各像元的局地太阳时显示出明显的分界线,导致LST在分界处存在突变,且存在部分空值. ...
针对MODIS影像的劈窗算法研究
1
2005
... (2)MOD11A1和MYD11A1地表温度和比辐射率产品,来自于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/).本研究从MOD11A1和MYD11A1产品[9 -10 ] 中提取LST、卫星过境时间和质量控制数据.其中如图2 所示,各像元的局地太阳时显示出明显的分界线,导致LST在分界处存在突变,且存在部分空值. ...
Thermal infrared(3~14 μm) bidirectional reflectance measurements of sands and soils
1
1997
... (3)MODIS的每日陆地温度发射率产品数据集(MOD11B1/MYD11B1),下载于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/).该产品时空分辨率分别为每天6 km,对数据集中的20、22、23、29、31、32波段的发射率进行合成[11 -12 ] ,得到地面气象观测站点对应像元的宽波段发射率. ...
BRDF models to predict spectral refle-ctance and emissivity in the thermal infrared
1
1998
... (3)MODIS的每日陆地温度发射率产品数据集(MOD11B1/MYD11B1),下载于NASA网站(https:∥ladsweb.modaps.eosdis.nasa.gov/).该产品时空分辨率分别为每天6 km,对数据集中的20、22、23、29、31、32波段的发射率进行合成[11 -12 ] ,得到地面气象观测站点对应像元的宽波段发射率. ...
Downscaling land surface temperature in an arid area by using multiple remote sensing indices with random forest regression
1
2017
... (4)地面气象站点实测数据.使用该数据集中的上下行长波辐射以及由步骤(3)估算的MODIS宽波段发射率集,基于Stefan-Boltzmann定律计算3个气象站点的地表温度[13 ] .获取的地表温度以验证FY4A_AGRI_L2_LST产品空值插补精度、BDTNM模型的时间归一化精度和MODIS LST产品时间归一化精度,从而评估BDTNM模型的时间归一化性能.该数据集由寒区旱区科学数据中心(http:∥westdc.westgis.ac.cn/zh-hans/)提供. ...
顾及时空特征的 FY‐4A 云覆盖像元地表温度重建模型
1
2021
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
顾及时空特征的 FY‐4A 云覆盖像元地表温度重建模型
1
2021
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
On the blending of the landsat and MODIS surface reflectance: predicting daily landsat surface reflectance
2
2006
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
... 使用空值填补后的一日内n 个FY⁃4A LST数据,依据Duan等的研究[4 ,15 ] 设置模型参数的初值,采用Levenberg-Marquardt非线性最小二乘方法进行拟合计算得到了每个像元适用于FY⁃4A的6个参数的值(式(2) ),由此,得到FY⁃4A每个像元的地表温度日变化曲线(式(3) ): ...
GIDS 空间插值法估算云下地表温度
1
2012
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
GIDS 空间插值法估算云下地表温度
1
2012
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
面向风云静止卫星地表温度产品的缺失数据修复方法对比
1
2017
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
面向风云静止卫星地表温度产品的缺失数据修复方法对比
1
2017
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
Smoothing and differentiation of data by simplified least squares procedures
1
1964
... 研究基于顾及时空特征的LST重建模型[14 ] ,改进了其中空间域相似像元的筛选方法,对FY-4A的地表温度数据集进行空值重建.即首先利用临近天相同时间LST相似的特征[15 ] ,在时间窗口内加权计算,实现时间域内LST产品空值的部分插补;其次基于空间域空值重建方法,计算空间窗口内所有像元的有效LST时序与中心像元LST时序的标准差,然后计算所有临近像元的标准差均值,选取标准差小于均值的对应像元作为相似像元,在空间窗口内加权计算[16 -17 ] ,空间域内对LST产品进行空值插补.选定时间窗口大小为11天,空间窗口大小为3×3像元,通过时空插补的循环迭代,直至完成对所有无效像元的重建.最后对完成初步重建的LST数据集采用S-G滤波器[18 ] 方法进行去噪处理,实现LST产品空值像元的重建. ...
长三角城市群表面城市热岛日内逐时变化规律
1
2017
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
长三角城市群表面城市热岛日内逐时变化规律
1
2017
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
Evaluation of six land-surface diurnal temperature cycle models using clear-sky in situ and satel-lite data
1
2012
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
基于FY-2F数据的中国区域地表温度日变化模型评价及特征研究
3
2019
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
... 模拟数据时间归一化误差如表4 所示,其中未做归一化通过真实过境时刻tr 时的站点地表温度与归一化时刻tp 时的站点地表温度计算得来,即若不做时间归一化,用tr 时刻的地表温度来代替tp 时刻的地表温度,则导致RMSE 1 K左右、MAE 0.7 K左右的误差.使用INA08_2模型进行时间归一化,RMSE和MAE大于1 K;使用BDTNM模型进行时间归一化,RMSE为0.46 K、MAE为0.32 K,其中效果最好为黑河遥感站,效果较差是张掖湿地站.表明BDTNM模型能够较好地对地表温度数据进行时间归一化.其中,黑河遥感站的下垫面类型为草地,每天的温度波动较大,故未做归一化引起的误差在该站最大,而INA08模型本身描述日内温度变化信息的精度就不如其他的六参数DTC模型,且在草地裸地或稀疏植被这两种地表覆盖类型的拟合精度最差[21 ] ,因此,INA08_2模型时间归一化在黑河遥感站精度最低;由于FY-4A具有高时间分辨率,足够的观测量可以更加全面地观测到一日内的温度变化,且JNG06模型也具有较好的拟合精度,因此BDTNM模型在张掖湿地站表现出很好的精度.另外,两种方法均在大满超级站(玉米田)的精度均高于张掖湿地站(芦苇湿地),这是由于地表温度日变化模型在农用地具有最好的拟合精度[21 ] .其中,BDTNM是不同站点之间精度差异较小,这是由于粗细像元之间的转换系数求解的精度几乎不受下垫面类型的影响.综上所述,BDTNM模型对地表温度的时间归一化的精度受下垫面类型的影响较小. ...
... [21 ].其中,BDTNM是不同站点之间精度差异较小,这是由于粗细像元之间的转换系数求解的精度几乎不受下垫面类型的影响.综上所述,BDTNM模型对地表温度的时间归一化的精度受下垫面类型的影响较小. ...
基于FY-2F数据的中国区域地表温度日变化模型评价及特征研究
3
2019
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
... 模拟数据时间归一化误差如表4 所示,其中未做归一化通过真实过境时刻tr 时的站点地表温度与归一化时刻tp 时的站点地表温度计算得来,即若不做时间归一化,用tr 时刻的地表温度来代替tp 时刻的地表温度,则导致RMSE 1 K左右、MAE 0.7 K左右的误差.使用INA08_2模型进行时间归一化,RMSE和MAE大于1 K;使用BDTNM模型进行时间归一化,RMSE为0.46 K、MAE为0.32 K,其中效果最好为黑河遥感站,效果较差是张掖湿地站.表明BDTNM模型能够较好地对地表温度数据进行时间归一化.其中,黑河遥感站的下垫面类型为草地,每天的温度波动较大,故未做归一化引起的误差在该站最大,而INA08模型本身描述日内温度变化信息的精度就不如其他的六参数DTC模型,且在草地裸地或稀疏植被这两种地表覆盖类型的拟合精度最差[21 ] ,因此,INA08_2模型时间归一化在黑河遥感站精度最低;由于FY-4A具有高时间分辨率,足够的观测量可以更加全面地观测到一日内的温度变化,且JNG06模型也具有较好的拟合精度,因此BDTNM模型在张掖湿地站表现出很好的精度.另外,两种方法均在大满超级站(玉米田)的精度均高于张掖湿地站(芦苇湿地),这是由于地表温度日变化模型在农用地具有最好的拟合精度[21 ] .其中,BDTNM是不同站点之间精度差异较小,这是由于粗细像元之间的转换系数求解的精度几乎不受下垫面类型的影响.综上所述,BDTNM模型对地表温度的时间归一化的精度受下垫面类型的影响较小. ...
... [21 ].其中,BDTNM是不同站点之间精度差异较小,这是由于粗细像元之间的转换系数求解的精度几乎不受下垫面类型的影响.综上所述,BDTNM模型对地表温度的时间归一化的精度受下垫面类型的影响较小. ...
Land surface emissivity retrieval from combined mid-Infrared and thermal infrared data of MSGSEVIRI
1
2006
... 经验统计的DTC模型通常使用分段函数来描述地表温度在一个昼夜周期中的变化,常见的简单DTC模型主要包括GOT01模型(5个参数)、VAN06模型(6个参数)、JNG06模型(6个参数)、INA08模型(5个参数)、GOT09模型(6个参数)以及其他基于地表能量平衡模拟的复杂模型(参数数量较多),这些模型都具有较好的物理基础与模拟精度[19 -20 ] .孟翔晨等[21 ] 在2018年对利用FY-2F数据评价了6种地表温度日变化模型在中国区的模拟精度,认为Jiang等[22 ] 在2006年提出的DTC模型(JNG06),具有较好的物理基础和更好的精度.故本研究选取JNG06模型来描述FY-4A地表温度的日变化信息.具体为: ...
Creating a seamless 1 km resolution daily land surface temperature dataset for urban and surrounding areas in the conterminous United States
1
2018
... 地表温度在短时间内的变化是可以看作是线性的[23 ] ,可以认为不同空间分辨率的LST之间的关系在短时间内是相似恒定的,即认为短时间内m 和q 不会变化. ...
Land surface temperature retrieval at high spatial and temporal resolutions over the Southwestern United States
1
2008
... 研究使用BDTNM模型对DOY267-273内28次过境的MODIS数据进行了时间归一化;并将INA08模型[24 ] 参数ts 固定为日落时间tss 前一小时,使用MODIS一日4次的数据建立INA08_2模型,对MODIS LST数据进行时间归一化[4 ] .利用研究区内3个站点的实测数据对两种方法的归一化结果进行精度评价. ...